初中数学北师大版九年级下学期第二章 2.5 二次函数与一元二次方程

试卷更新日期：2020-03-04 类型：同步测试

进入出卷网下载

1. 抛物线y=x²+2x+3与y轴的交点为（）

A、(0，2) B、(2，0) C、(0，3) D、(3，0)

查看试题解析
2. 已知二次函数y=ax²+bx+c(a≠0)图象上部分点的坐标(x，y)的对应值如下表所示：

x

…

0

$\sqrt{5}$

4

…

y

…

0.37

-1

0.37

…

则方程ax²+bx+1.37=0的根是（）

A、0或4 B、 $\sqrt{5}$ 或4- $\sqrt{5}$ C、1或5 D、无实根

查看试题解析
3. 已知函数y=（k-1）x²-4x+4与x轴只有一个交点，则k的取值范围是（）

A、 $k \leq 2$ 且 $k \neq 1$ B、 $k < 2$ 且 $k \neq 1$ C、 $k = 2$ D、 $k = 2$ 或1

查看试题解析
4. 已知函数 $y = 3 - (x - m) (x - n)$ ，并且 $a$ ， $b$ 是方程 $3 - (x - m) (x - n) = 0$ 的两个根，则实数 $m$ ， $n$ ， $a$ ， $b$ 的大小关系可能是（）

A、 $m < n < b < a$ B、 $m < a < n < b$ C、 $a < m < b < n$ D、 $a < m < n < b$

查看试题解析
5. 已知函数 $y = a x^{2} + b x + c (a \neq 0)$ ，其几对对应值如表，判断方程 $a x^{2} + b x + c = 0 (a \neq 0 ， a ， b ， c$ 为常数）的根的个数（　　）

$x$

6.17

6.18

6.19

6.20

$y$

0.02

-0.01

0.02

0.04

A、0 B、1 C、2 D、1或2

查看试题解析
6. 若关于x的方程x²﹣mx+n＝0没有实数解，则抛物线y＝x²﹣mx+n与x轴的交点有（）

A、2个 B、1个 C、0个 D、不能确定

查看试题解析

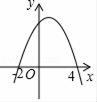
7. 抛物线y=x²-9与y轴的交点坐标为。

查看试题解析
8. 如图，二次函数y=ax²+bx+c的图象与x轴交于（﹣2，0）和（4，0）两点，当函数值y＞0时，自变量x的取值范围是

查看试题解析
9. 抛物线 $y = x^{2} - 2 x - 1$ 与 $x$ 轴有个交点．

查看试题解析
10. 已知关于x的方程2+（x﹣m）（x﹣n）＝0，存在a，b是方程2+（x﹣m）（x﹣n）＝0的两个根，则实数m，n，a，b的大小关系可能是.

查看试题解析
11. 对于二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的描述，下列命题：①若 $a + b + c = 0$ ，则b²-4ac≥0；②若 $b = 2 a + 3 c$ ，则一元二次方程 $a x^{2} + b x + c = 0$ 有两个不相等的实数根；③若 $b^{2} - 4 a c > 0$ ，则二次函数 $y = a x^{2} + b x + c$ 的图象与坐标轴的公共点的个数是2或3；④若 $b > a + c$ ，则一元二次方程 $a x^{2} + b x + c = 0$ 有两个不相等的实数根．其中结论正确的有（填写所有正确的序号）.

查看试题解析
12. 如图是二次函数y＝﹣x²+4x的图象，若关于x的一元二次方程﹣x²+4x﹣t＝0（t为实数）在1＜x＜5的范围内有解，则t的取值范围是．

查看试题解析
13. 二次函数y=﹣2x²﹣3x+k的图象在x轴下方，则k的取值范围是．

查看试题解析

x	…	0	$\sqrt{5}$	4	…
y	…	0.37	-1	0.37	…

$x$	6.17	6.18	6.19	6.20
$y$	0.02	-0.01	0.02	0.04

初中数学北师大版九年级下学期 第二章 2.5 二次函数与一元二次方程