初中数学北师大版九年级下学期 第二章 2.4 二次函数的应用
试卷更新日期：2020-03-04 类型：同步测试
一、单选题
-
1. 如图，以40m/s的速度将小球沿与地面成30°角的方向击出时，小球的飞行路线将是一条抛物线．如果不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有函数关系h＝20t﹣5t2 ． 下列叙述正确是（ ）
A、小球的飞行高度不能达到15m B、小球的飞行高度可以达到25m C、小球从飞出到落地要用时4s D、小球飞出1s时的飞行高度为10m2. 为了改善居民住房条件，某市计划用未来两年的时间，将城镇居民的住房面积由现在的人均约为20平方米提高到28.8平方米，若每年的年增长率相同，设年增长率为x,则下面列出的方程中正确的是（ ）A、 B、 C、 D、3. 教练对小明推铅球的录像进行技术分析，发现某次铅球行进高度y(m)与水平距离x(m)之间的关系为y=- (x-4)2+3，由此可知小明这次的推铅球成绩是（ ）A、3m B、4m C、8m D、10m4. 若抛物线y=x2-4x-12与x轴交于点A，B，与y轴交于点C，则△ABC的面积为（ ）A、24 B、36 C、48 D、965. 如图，利用一个直角墙角修建一个梯形储料场ABCD，其中∠C＝120°.若新建墙BC与CD总长为12m，则该梯形储料场ABCD的最大面积是（ ）
A、18m2 B、 m2 C、 m2 D、 m26. 一种包装盒的设计方法如图所示，四边形ABCD是边长为30cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A，B，C，D四点重合于图中的点O，形成一个底面为正方形的长方体包装盒．设BE=CF=xcm，要使包装盒的侧面积最大，则x应取（ ）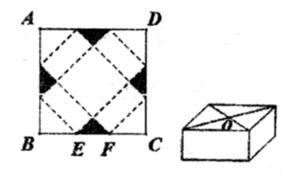
A、12.5cm B、10cm C、7.5cm D、5cm7. 超市有一种”喜之郎”果冻礼盒，内装两个上下倒置的果冻，果冻高为4cm，底面是个直径为6cm的圆，轴截面可以近似地看作一个抛物线，为了节省成本，包装应尽可能的小，这个包装盒的长AD(不计重合部分，两个果冻之间没有挤压)至少为（ ）
A、(6+3 )cm B、(6+2 )cm C、(6+2 )cm D、(6+3 )cm二、填空题
-
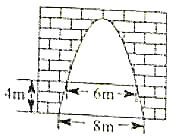
8. 如图，有一个横截面边缘为抛物线的水泥门洞，门洞内的地面宽度为 ，两侧离地面 高处各有一盏灯，两灯间的水平距离为 ，则这个门洞的高度为 .（精确到 ）
9. 小强推铅球时，铅球的高度y(m)与水平行进的距离x(m)之间的关系为y= (x-4)2+3，则小强推铅球的成绩是m。三、综合题
-
10. 某经销商以每千克30元的价格购进一批原材料加工后出售，经试销发现，每天的销售量y（千克）与销售单价x（元/千克）符合一次函数y＝kx+b，且x＝35时，y＝55；x＝42时，y＝48．(1)、求一次函数y＝kx+b的表达式；(2)、设该商户每天获得的销售利润为W（元），求出利润W（元）与销售单价x（元/千克）之间的关系式；(3)、销售单价每千克定为多少元时，商户每天可获得最大利润？最大利润是多少元？（销售利润＝销售额﹣成本）11. 如图，已知二次函数 的图像与x轴交于A、B两点(点A在点B左侧)，与y轴交于点C．
(1)、求线段BC的长；(2)、当0≤y≤3时，请直接写出x的范围；(3)、点P是抛物线上位于第一象限的一个动点，连接CP，当∠BCP＝90o时，求点P的坐标．12. 金秋时节，硕果飘香，某精准扶贫项目果园上市一种有机生态水果，为帮助果园拓宽销路。欣欣超市对这种水果进行代销，进价为5元／千克，售价为6元／千克时，当天的销售量为60千克；在销售过程中发现：销售单价每上涨0.5元，当天的销售量就减少5千克．设当天销售单价统一为x元／千克(x≥6，且x按0.5元的倍数上涨)，当天销售利润为y元。(1)、求y与x的函数关系式；(2)、若该种水果每千克的利润不超过80％，求当天获得利润的范围。13. 某小区为了改善居住环境，准备修建一个巨型花园ABCD，为了节约材料并种植不同花卉，决定花园一边靠墙，三边用栅栏围住，中间用一段垂直于墙的栅栏隔成两块.已知所用栅栏的总长为60米，墙长为30米，设花园垂直于墙的一边的长为 米.
(1)、若平行于墙的一边长为 米，直接写出 与 的函数关系式及自变量
的取值范围； (2)、当 为何值时，这个矩形花园的面积最大？最大值为多少？（栅栏占地面积忽略不计）(3)、当这个花园的面积不小于288平方米时，试结合函数图象，直接写出 的取值范围