初中数学北师大版九年级下学期第二章 2.3 确定二次函数的表达式-在线组卷题库

1. 抛物线 $y = 2 x^{2} + c$ 的顶点坐标为(0，1)，则抛物线的解析式为（）

A、 $y = 2 x^{2} + 1$ B、 $y = 2 x^{2} - 1$ C、 $y = 2 x^{2} + 2$ D、 $y = 2 x^{2} - 2$

查看试题解析
2. 已知二次函数的图象如图所示，则这个二次函数的表达式为（）

A、 $y = x^{2} - 2 x + 3$ B、 $y = x^{2} - 2 x - 3$ C、 $y = x^{2} + 2 x - 3$ D、 $y = x^{2} + 2 x + 3$

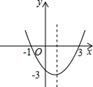查看试题解析
3. 二次函数的部分图象如图所示，对称轴是x=﹣1，则这个二次函数的表达式为（）

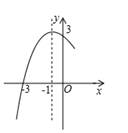A、y=﹣x²+2x+3 B、y=x²+2x+3 C、y=﹣x²﹣2x+3 D、y=﹣x²+2x﹣3

查看试题解析
4. 与抛物线y＝－ $\frac{4}{5}$ x²－1顶点相同，形状也相同，而开口方向相反的抛物线所对应的函数解析式是（）

A、y＝－ $\frac{4}{5}$ x²－1 B、y＝ $\frac{4}{5}$ x²－1 C、y＝－ $\frac{4}{5}$ x²＋1 D、y＝ $\frac{4}{5}$ x²＋1

查看试题解析

5. 已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 图象的顶点为 $P (- 2, 3)$ ，且过 $A (- 3, 0)$ ，则抛物线的关系式为．

查看试题解析
6. 运动员将小球沿与地面成一定角度的方向击出，在不考虑空气阻力的条件下，小球的飞行高度h（m）与它的飞行时间t（s）满足二次函数关系，t与h的几组对应值如下表所示．

t（s）

0

0.5

1

1.5

2

…

h（m）

0

8.75

15

18.75

20

…

则h与t之间的函数关系式（不要求写t的取值范围）为

查看试题解析

7. 已知抛物线y=-x²+bx+c过点(4，0)，点(1，3)，求此抛物线的解析式。

查看试题解析
8. 已知二次函数的图象与x轴交于点(－1，0)和 (3，0)，并且与y轴交于点(0，3)．求这个二次函数表达式．

查看试题解析
9. 设二次函数y=x²+bx+c(b，c是实数)，甲求得当x=0时，y=-2；当x=1时，y=0；乙求得当x=-2时，y=0．若甲求得的结果都正确，你认为乙求得的结果正确吗？说明理由。

查看试题解析

初中数学北师大版九年级下学期第二章 2.3 确定二次函数的表达式

t（s）	0	0.5	1	1.5	2	…
h（m）	0	8.75	15	18.75	20	…