辽宁省鞍山市台安县2019-2020学年八年级上学期数学第二次月考试卷

试卷更新日期：2020-03-04 类型：月考试卷

进入出卷网下载

一、单选题

1. 改革开放以来，我国众多科技实体在各自行业取得了举世瞩目的成就，大疆科技、华为集团、太极股份和凤凰光学等就是其中的杰出代表．上述四个企业的标志是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在平面直角坐标系中，点B的坐标是（4，﹣1），点A与点B关于x轴对称，则点A的坐标是（）

A、（4，1） B、（﹣1，4） C、（﹣4，﹣1） D、（﹣1，﹣4）

查看试题解析
3. 已知三角形的两边分别为1和4，第三边长为整数，则该三角形的周长为（）

A、7 B、8 C、9 D、10

查看试题解析
4. 将一副直角三角板按如图所示的位置摆放，使得它们的直角边互相垂直，则 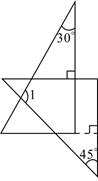$∠ 1$ 的度数是（）

A、 $95 °$ B、 $100 °$ C、 $105 °$ D、 $110 °$

查看试题解析
5. 下列运算正确的是（）

A、 ${(a b)}^{2} = a^{2} b^{2}$ B、 $a^{2} + a^{2} = a^{4}$ C、 ${(a^{2})}^{3} = a^{5}$ D、 $a^{2} \cdot a^{3} = a^{6}$

查看试题解析
6. 下列等式从左到右的变形是因式分解的是（）

A、6x（3x﹣1）＝18 $x^{2}$ ﹣6x B、（2x﹣3）（2x+3）＝4 $x^{2}$ ﹣9 C、 $x^{2}$ ﹣6x+9＝（x﹣3）² D、2 $x^{2}$ +3x+1＝x（2x+3）+1

查看试题解析
7. 如图，点A，E，F，D在同一直线上，若AB∥CD，AB=CD，AE=FD，则图中的全等三角形有（）

A、1对 B、2对 C、3对 D、4对

查看试题解析
8. 如图，已知在四边形ABCD中，∠BCD=90°，BD平分∠ABC，AB=6，BC=9，CD=4，则四边形ABCD的面积是（）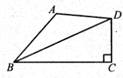

A、24 B、30 C、36 D、42

查看试题解析

二、填空题

9. 计算： $a^{6} \div a^{2} =$ _.

查看试题解析
10. 一个 $n$ 边形从一个顶点出发引出的对角线可将其分割成5个三角形，则 $n$ 的值为.

查看试题解析
11. 如图，在 $Δ A B C$ 中， $C D$ 平分 $∠ A C B$ ， $D E / / B C$ ，交 $A C$ 于点 $E$ ，若 $∠ A = 60 °$ ， $∠ B = 70 °$ ，则 $∠ D$ 的度数为.

查看试题解析
12. 多项式 $6 a^{3} b^{2} - 3 a^{2} b^{3}$ 因式分解时，应提取的公因式是.

查看试题解析
13. 把多项式 $2 x^{2} - 8$ 分解因式的结果是.

查看试题解析
14. 如图，已知∠1=∠2，AC=AD，请增加一个条件，使△ABC≌△AED，你添加的条件是.

查看试题解析
15. 如图，在 $Δ A B C$ 中， $∠ A B C = 120 °$ ， $A B = B C$ ，过 $A B$ 的中点 $M$ 作 $M N ⊥ A B$ ，交 $A C$ 于点 $N$ .若 $A C = 12 c m$ ，则 $C N =$ $c m$ .

查看试题解析
16. 已知：如图，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA，过E作EF⊥AB，F为垂足，下列结论：①△ABD≌△EBC；②∠BCE+∠BCD=180°；③AD=EF=EC；④AE=EC，其中正确的是(填序号)

查看试题解析

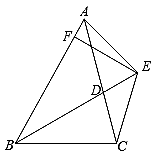
三、解答题

17. 分解因式： $m^{3} n - 9 m n$

查看试题解析
18. 分解因式： $- a^{3} b + 2 a^{2} b - a b$

查看试题解析
19. 已知 $a + b = 3, a b = - 1$ ，求 ${(a - b)}^{2}$

查看试题解析
20. 先化简，再求值： $(2 m + 1) (2 m - 1) - {(m - 1)}^{2} + {(2 m)}^{3} \div (- 8 m)$ ，其中 $m^{2} + m - 2 = 0$

查看试题解析
21. 先阅读下列材料，再解答下列问题：
材料：因式分解： ${(x + y)}^{2} + 2 (x + y) + 1$

解：将“ $x + y$ ”看成整体，令 $x + y = A$ ，则原式 $= A^{2} + 2 A + 1 = {(A + 1)}^{2}$

将 “ $A$ ”还原，得原式 $= {(x + y + 1)}^{2}$

上述解题过程用到的是“整体思想”，“整体思想”是数学解题中常用的一种思想方法，请你解答下问题：

(1)、因式分解： $1 + 2 (x - y) + {(x - y)}^{2} =$ ；

(2)、因式分解： $(a + b) (a + b - 4) + 4$

查看试题解析
22. 如图，已知六边形 $A B C D E F$ 的每个内角都相等，连接 $A D$ .

(1)、若 $∠ 1 = 48 °$ ，求 $∠ 2$ 的度数；

(2)、求证： $A B / / D E$ .

查看试题解析
23. 如图，在 $Δ A B C$ 和 $Δ D B C$ 中， $∠ A C B = ∠ D B C = 90 °$ ， $E$ 是 $B C$ 的中点， $E F ⊥ A B$ 于点 $F$ ，且 $A B = D E$ .

(1)、求证： $B C = D B$ ；

(2)、若 $D B = 8 c m$ ，求 $A C$ 的长.

查看试题解析
24. 如图，已知点A、C分别在∠GBE的边BG、BE上，且AB=AC，AD∥BE，∠GBE的平分线与AD交于点D，连接CD.

(1)、求证：①AB=AD； ②CD平分∠ACE.

(2)、猜想∠BDC与∠BAC之间有何数量关系？并对你的猜想加以证明.

查看试题解析
25. $Δ A B C$ 与 $Δ D C E$ 有公共顶点 $C$ （顶点均按逆时针排列）， $A B = A C$ ， $D C = D E$ ， $∠ B A C + ∠ C D E = 180 °$ ， $D E / / B C$ ，点 $G$ 是 $B E$ 的中点，连接 $D G$ 并延长交直线 $B C$ 于点 $F$ ，连接 $A F ， A D$ .

(1)、如图，当 $∠ B A C = 90 °$ 时，
求证：① $B F = C D$ ；

② $Δ A F D$ 是等腰直角三角形.

(2)、当 $∠ B A C = 60 °$ 时，画出相应的图形（画一个即可），并直接指出 $Δ A F D$ 是何种特殊三角形.

查看试题解析