江苏省宜兴市丁蜀学区渎边联盟2019-2020学年八年级上学期数学第二次月考试卷
试卷更新日期:2020-03-04 类型:月考试卷
一、单选题
-
1. 甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,不是轴对称的是( )A、
 B、
B、 C、
C、 D、
D、 2. 点(2,-3)关于y轴对称的点的坐标是( )A、(-2,3) B、(-2,-3) C、(2,3) D、(2,-3)3. 已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )
2. 点(2,-3)关于y轴对称的点的坐标是( )A、(-2,3) B、(-2,-3) C、(2,3) D、(2,-3)3. 已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )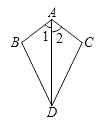 A、AB=AC B、BD=CD C、∠B=∠C D、∠BDA=∠CDA4. 下列选项中,与数轴上的点一一对应的是( )A、实数 B、有理数 C、正整数和0 D、无理数5. 到三角形三条边距离相等的点是( )A、三条角平分线的交点 B、三边中线的交点 C、三边上高所在直线的交点 D、三边的垂直平分线的交点6. 一次函数 y = mx + 的图像过点(0,2),且 y 随 x 的增大而增大,则 m 的值为( )A、-1 B、3 C、1 D、- 1 或 37. 下列命题: (1) =a,(2) =a,(3)无限小数都是无理数,(4)有限小数都是有理数,(5)实数分为正实数和负实数两类.正确的有( )A、1个 B、2个 C、3个 D、4个8. 下列关于一次函数y=﹣2x+3的结论中,正确的是( )A、图象经过点(3,0) B、图象经过第二、三、四象限 C、y随x增大而增大 D、当x> 时,y<09. 如图,正方形ABCD的边长为3,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )
A、AB=AC B、BD=CD C、∠B=∠C D、∠BDA=∠CDA4. 下列选项中,与数轴上的点一一对应的是( )A、实数 B、有理数 C、正整数和0 D、无理数5. 到三角形三条边距离相等的点是( )A、三条角平分线的交点 B、三边中线的交点 C、三边上高所在直线的交点 D、三边的垂直平分线的交点6. 一次函数 y = mx + 的图像过点(0,2),且 y 随 x 的增大而增大,则 m 的值为( )A、-1 B、3 C、1 D、- 1 或 37. 下列命题: (1) =a,(2) =a,(3)无限小数都是无理数,(4)有限小数都是有理数,(5)实数分为正实数和负实数两类.正确的有( )A、1个 B、2个 C、3个 D、4个8. 下列关于一次函数y=﹣2x+3的结论中,正确的是( )A、图象经过点(3,0) B、图象经过第二、三、四象限 C、y随x增大而增大 D、当x> 时,y<09. 如图,正方形ABCD的边长为3,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )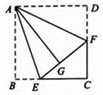 A、 B、 C、 D、3
A、 B、 C、 D、3二、填空题
-
10. 若点A(x,2)在第二象限,则x的取值范围是
11. 若 ,则以 为边长的等腰三角形的周长为 .12. 将一次函数 的图象向下平移3个单位长度,相应的函数表达式为 .13. 我市市域面积约为1996.6平方公里,数据1996.6用四舍五入法精确到百位,可以用科学记数法表示为.14. 在△ABC中,边AB的垂直平分线分别交AB、AC于点D,E,若AD为4㎝,△ABC的周长为26㎝,则△BCE的周长为㎝.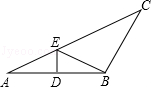 15. 若函数y=4x+b的图象与两坐标轴围成的三角形面积为2,则b=16. 如图,在直角坐标系中,点A、B的坐标分别为(2,4)和(3、0)点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,在运动的过程中,当△ABC是以AB为底的等腰三角形时,此时点C的坐标为 .
15. 若函数y=4x+b的图象与两坐标轴围成的三角形面积为2,则b=16. 如图,在直角坐标系中,点A、B的坐标分别为(2,4)和(3、0)点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,在运动的过程中,当△ABC是以AB为底的等腰三角形时,此时点C的坐标为 .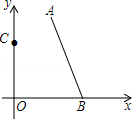
三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 求x的值:(1)、 ;(2)、 .19. 已知:如图,AC与BD相交于点O,AC⊥BC,AD⊥BD,垂足分别为点C、D,且AC=BD.求证:OA=OB.
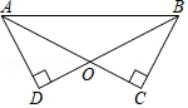 20. 如图,△ABC三个顶点的坐标分别为A(4,5)、B(1,0)、C(4,0).
20. 如图,△ABC三个顶点的坐标分别为A(4,5)、B(1,0)、C(4,0). (1)、画出△ABC关于y轴的对称图形△A1B1C1 , 并写出A1点的坐标;(2)、在y轴上求作一点P,使△PAB的周长最小,并求出点P的坐标及△PAB的周长最小值.21. 已知:y+2与x﹣3成正比例,且当x=5时,y=2.(1)、求y与x之间的函数表达式;(2)、当y=4时,x的值是多少?22. 课间,小明拿着老师的等腰直角三角板玩,不小心掉到两墙之间,如图 , .
(1)、画出△ABC关于y轴的对称图形△A1B1C1 , 并写出A1点的坐标;(2)、在y轴上求作一点P,使△PAB的周长最小,并求出点P的坐标及△PAB的周长最小值.21. 已知:y+2与x﹣3成正比例,且当x=5时,y=2.(1)、求y与x之间的函数表达式;(2)、当y=4时,x的值是多少?22. 课间,小明拿着老师的等腰直角三角板玩,不小心掉到两墙之间,如图 , .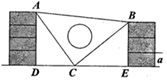 (1)、求证: ;(2)、若三角板的一条直角边 ,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).23. 已知一次函数 的图像经过点 ,且与正比例函数 的图像相交于点 .(1)、求m的值;(2)、求一次函数 的解析式;(3)、求这两个函数图象与x轴所围成的三角形面积.24. 小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min.设小明出发x min后行走的路程为y m.图中的折线表示小明在整个行走过程中y与x的函数关系.
(1)、求证: ;(2)、若三角板的一条直角边 ,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).23. 已知一次函数 的图像经过点 ,且与正比例函数 的图像相交于点 .(1)、求m的值;(2)、求一次函数 的解析式;(3)、求这两个函数图象与x轴所围成的三角形面积.24. 小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min.设小明出发x min后行走的路程为y m.图中的折线表示小明在整个行走过程中y与x的函数关系. (1)、小明行走的总路程是m,他途中休息了min.
(1)、小明行走的总路程是m,他途中休息了min.
(2)、①当60≤x≤90时,求y与x的函数关系式;②当小丽到达缆车终点时,小明离缆车终点的路程是多少?
25. 在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG. (1)、求∠DFG的度数;(2)、设∠BAD=θ,
(1)、求∠DFG的度数;(2)、设∠BAD=θ,①当θ为何值时,△DFG为等腰三角形;
②△DFG有可能是直角三角形吗?若有,请求出相应的θ值;若没有,请说明理由.