江苏省兴化市顾庄学区2019-2020学年八年级上学期数学12月月考试卷
试卷更新日期:2020-03-04 类型:月考试卷
一、单选题
-
1. 下列四个图形中轴对称图形的个数是( )
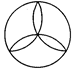


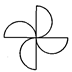 A、1 B、2 C、3 D、42. 已知点P(0,a)在y轴的负半轴上,则点Q(﹣a2﹣1,﹣a+1)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列实数0, , ,π,其中,无理数共有( )A、1个 B、2个 C、3个 D、4个4. 下列等式正确的是( )A、 B、 C、 D、5. 等腰三角形两边长分别是2 cm和5 cm,则这个三角形周长是( )A、9 cm B、12 cm C、9 cm或12 cm D、14 cm6. 6月1日起,我国将全面试行居民阶梯式电价,某市出台了实施细则,具体规定如下:
A、1 B、2 C、3 D、42. 已知点P(0,a)在y轴的负半轴上,则点Q(﹣a2﹣1,﹣a+1)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列实数0, , ,π,其中,无理数共有( )A、1个 B、2个 C、3个 D、4个4. 下列等式正确的是( )A、 B、 C、 D、5. 等腰三角形两边长分别是2 cm和5 cm,则这个三角形周长是( )A、9 cm B、12 cm C、9 cm或12 cm D、14 cm6. 6月1日起,我国将全面试行居民阶梯式电价,某市出台了实施细则,具体规定如下:设用电量为a度,当a≤150时,电价为现行电价,每度0.51元;当150<a≤240时,在现行电价基础上,每度提高0.05元;当a>240时,在现行电价基础上,每度提高0.30元.设某户的月用电量为x(度),电费为y(元).则y与x之间的函数关系的大致图像是( )
A、 B、
B、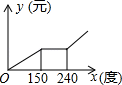 C、
C、 D、
D、
二、填空题
-
7. a的平方根是±3,那么a=.8. 函数y= 中,自变量x的取值范围是;实数2﹣ 的倒数是 .9. 已知点P(2a+b,b)与P1(8,﹣2)关于y轴对称,则a+b=.10. 近似数13.7万精确到位.11. 已知一次函数的图象与直线y=﹣x+1平行,且过点(8,2),那么此一次函数的解析式为.12. 已知在△ABC中,∠C=90°,AC=3,BC=4,分别以AC、BC、AB为直径作半圆,如图所示,则阴影部分的面积是.
 13. 在平面直角坐标系中,若点M(2,4)与点N(x,4)之间的距离是3,则x的值是.14. 如图,在平面直角坐标系中,点P(﹣1,a)在直线y=2x+2与直线y=2x+4之间,则a的取值范围是.
13. 在平面直角坐标系中,若点M(2,4)与点N(x,4)之间的距离是3,则x的值是.14. 如图,在平面直角坐标系中,点P(﹣1,a)在直线y=2x+2与直线y=2x+4之间,则a的取值范围是. 15. 已知:如图△ABC中,∠B=50°,∠C=90°,在射线BA上找一点D,使△ACD为等腰三角形,则∠ACD的度数为.
15. 已知:如图△ABC中,∠B=50°,∠C=90°,在射线BA上找一点D,使△ACD为等腰三角形,则∠ACD的度数为. 16. 如图,已知直线AB与x轴交于点A(4,0)、与y轴交于点B(0,3),直线 BD与x轴交于点D,将直线AB沿直线BD翻折,点A恰好落在y轴上的C点,则直线BD对应的函数关系式为 .
16. 如图,已知直线AB与x轴交于点A(4,0)、与y轴交于点B(0,3),直线 BD与x轴交于点D,将直线AB沿直线BD翻折,点A恰好落在y轴上的C点,则直线BD对应的函数关系式为 .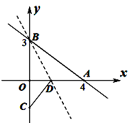
三、解答题
-
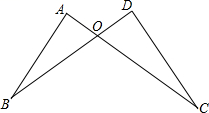
17. 计算: .18. 求下列各式中x的值:(1)、2x2-32=0;(2)、(x+4)3+64=0.19. 已知2m+2的平方根是±4,3m+n+1的平方根是±5,求m+2n的立方根.20. 如图,已知 AB=DC,AC=DB,AC 和 DB 相交于点 O. 求证:OB=OC.
 21. 如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高?
21. 如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高? 22.(1)、在网格中画 ,使 、 、 三边的长分别为 、 、
22.(1)、在网格中画 ,使 、 、 三边的长分别为 、 、 (2)、判断三角形的形状:(直接填结论).(3)、求 的面积.23. 已知一次函数y=kx+b的图象经过点(﹣2,﹣4),且与正比例函数 的图象相交于点(4,a),求:
(2)、判断三角形的形状:(直接填结论).(3)、求 的面积.23. 已知一次函数y=kx+b的图象经过点(﹣2,﹣4),且与正比例函数 的图象相交于点(4,a),求: (1)、a的值;(2)、k、b的值;(3)、画出这两个函数图象,并求出它们与y轴相交得到的三角形的面积.24. 某厂家在甲、乙两家商场销售同一商品所获得的利润分别为 , (单位:元), , 与销售数量x(单位:件)的函数关系如图所示,试根据图象解决下列问题:
(1)、a的值;(2)、k、b的值;(3)、画出这两个函数图象,并求出它们与y轴相交得到的三角形的面积.24. 某厂家在甲、乙两家商场销售同一商品所获得的利润分别为 , (单位:元), , 与销售数量x(单位:件)的函数关系如图所示,试根据图象解决下列问题: (1)、分别求出 , 关于x的函数关系式;(2)、现厂家分配该商品800件给甲商场,400件给乙商场,当甲、乙商场售完这批商品后,厂家可获得的总利润是多少元?25. 已知等腰Rt△ABC中,∠BAC=90°.点D从点B出发在线段BC移动,以AD为腰作等腰Rt△ADE,∠DAE=90°.连接CE.
(1)、分别求出 , 关于x的函数关系式;(2)、现厂家分配该商品800件给甲商场,400件给乙商场,当甲、乙商场售完这批商品后,厂家可获得的总利润是多少元?25. 已知等腰Rt△ABC中,∠BAC=90°.点D从点B出发在线段BC移动,以AD为腰作等腰Rt△ADE,∠DAE=90°.连接CE. (1)、如图,求证:△ACE≌△ABD;(2)、求证:BD2+CD2=2AD2;(3)、若AB=4,试问:△DCE的面积有没有最大值,如没有请说明理由,如有请求出最大值.26. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
(1)、如图,求证:△ACE≌△ABD;(2)、求证:BD2+CD2=2AD2;(3)、若AB=4,试问:△DCE的面积有没有最大值,如没有请说明理由,如有请求出最大值.26. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:

 (1)、请问甲乙两地的路程为;(2)、求慢车和快车的速度;(3)、求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;(4)、如果设慢车行驶的时间为x(h),快慢两车到乙地的距离分别为y1(km)、y2(km),请在右图中画出y1、y2与x的函数图象.
(1)、请问甲乙两地的路程为;(2)、求慢车和快车的速度;(3)、求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;(4)、如果设慢车行驶的时间为x(h),快慢两车到乙地的距离分别为y1(km)、y2(km),请在右图中画出y1、y2与x的函数图象.