江苏省南京市江宁区五校2019-2020学年八年级上学期数学12月月考试卷
试卷更新日期：2020-03-04 类型：月考试卷
一、单选题
-
1. 下列图形中，不一定是轴对称图形的是（ ）A、角 B、等腰三角形 C、平行四边形 D、长方形2. 4的平方根是（ ）A、 B、－ C、±4 D、±23. 在 ， ， ， ， ，0这六个数中，无理数的个数有（ ）A、1个 B、2个 C、3个 D、4个4. 一次函数 的图象不经过（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 小明从家出发，外出散步，到一个公共阅报栏看了一会报后，继续散步了一段时间，然后回家.如图描述了小明在散步过程中离家的距离s（米）与离家后所用时间t（分）之间的函数关系.则下列说法中错误的是（ ）
A、小明看报用时8分钟 B、小明离家最远的距离为400米 C、小明从家到公共阅报栏步行的速度为50米/分 D、小明从出发到回家共用时16分钟6. 函数 的图象如图所示，则关于 的不等式 的解集是 （ ）
A、 B、 C、 D、二、填空题
-
7. 3的平方根是；写出一个比-2小的无理数.8. 比较大小： 2.9. 若直角三角形的两直角边长分别为5和12，则斜边上的中线长为 ．10. 地球的半径约为6.4×106m，这个近似数精确到m.11. 点（2，－3）关于坐标原点对称点的坐标是.12. 函数y= 的自变量x的取值范围为.13. 一次函数y=（k-1）x+1的函数值y随x的增大而增大，则k的取值范围是.14. 已知点P(a,b)在一次函数y=2x-1的图像上，则2a-b+1=.15. 一次函数y＝2x－1的图象沿y轴正方向平移3个单位长度，则平移后的图象所对应的函数表达式为.16. 如图，平面直角坐标系内有一点A（3，4），O为坐标原点.点B在x轴上，若△AOB为等腰三角形，则点B的坐标为.
三、解答题
-
17.(1)、计算： ；(2)、求x的值(x–2)2–3＝0.18. 如图，点D，E在△ABC的边BC上，AB=AC，BD=CE.求证：∠ADE=∠AED.
19. 如图，Rt△ABC中，AB＝AC，∠BAC＝90°，点O是BC的中点，如果点M、N分别在线段AB、AC上移动，并在移动过程中始终保持AN＝BM.
(1)、求证：△ANO≌△BMO；(2)、求证：OM⊥ON.20. 如图，平面直角坐标系中，一次函数y＝－2x＋1的图像与y轴交于点A.
(1)、若点A关于x轴的对称点B在一次函数y＝x＋b的图像上，求b的值，并在同一坐标系中画出该一次函数的图象；(2)、求这两个一次函数的图象与y轴围成的三角形的面积.21. 如图，Rt△ABC中，∠ACB＝90°.
(1)、作∠BAC的平分线，交BC于点D；（要求：尺规作图，不写作法，保留作图痕迹）(2)、在（1）的条件下，若BD＝5，CD＝3，求AC的长.22. 已知等腰三角形的周长为12.
(1)、写出底边长y关于腰长x的函数表达式（x为自变量）；(2)、写出自变量x的取值范围；(3)、在直角坐标系中，画出该函数的图象.23. 某种洗衣机在洗涤衣服时，经历了进水、清洗、排水、脱水四个连续的过程，其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示.根据图象解答下列问题：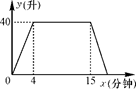
(1)、洗衣机的进水时间是多少分钟？清洗时洗衣机中水量为多少升？(2)、已知洗衣机的排水速度为每分钟19升.①求排水时洗衣机中的水量y(升)与时间x(分钟)与之间的关系式；
②如果排水时间为2分钟，求排水结束时洗衣机中剩下的水量.
24. 如图①所示，某乘客乘高速列车从甲地经过乙地到丙地，假设列车匀速行驶.如图②表示列车离乙地路程y（千米）与列车从甲出发后行驶时间x（小时）之间的函数关系图像.
(1)、甲、丙两地间的路程为千米；(2)、求高速列车离乙地的路程y与行驶时间x之间的函数关系式，并写出x的取值范围；(3)、当行驶时间x在什么范围时，高速列车离乙地的路程不超过100千米.25. 一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为 ，两车之间的距离为 ，图中的折线表示 与 之间的函数关系，根据图象进行一下探究：
(1)、信息读取甲、乙两地之间的距离为 ：
(2)、请解释图中点 的实际意义：(3)、图象理解求慢车和快车的速度：(4)、求线段 所表示的 与 之间的函数关系式，并写出自变量 的取值范围：(5)、问题解决若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同，在第一列快车与慢车相遇 分钟后，第二列快车与慢车相遇，求第二列快车比第一列快车晚出发多少小时？