江苏省东台市第二联盟2019-2020学年八年级上学期数学第三次月考试卷
试卷更新日期：2020-03-04 类型：月考试卷
一、单选题
-
1. 下面图案中是轴对称图形的有（ ）
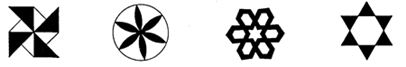A、1个 B、2个 C、3个 D、4个2. 在平面直角坐标系中，若点P的坐标为( ，-2)，则点P所在的象限是（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知等腰三角形的一个角是100°，则它的顶角是（ ）A、40° B、60° C、80° D、100°4. 下列计算正确的是（ ）A、－|－ |＝ B、 ＝±7 C、 ＝2 D、± ＝±25. 下列四组线段中，可以构成直角三角形的是（ ）A、6，8，10 B、4，5，6 C、2，3，4 D、1， ，36. 如图，已知 ， ，下列不能判定 的条件是（ ）.
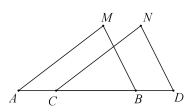A、 B、 C、 D、7. 如图，在△ABC中，AC的垂直平分线交AC于点E，交BC于点D，△ABD的周长为16cm，AC为5cm，则△ABC的周长为（ ）
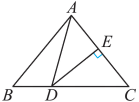A、24cm B、21cm C、20cm D、无法确定8. 在平面直角坐标系中，等腰△ABC的顶点A、B的坐标分别为(1，0)、(2，3)，若顶点C落在坐标轴上，则符合条件的点C有（ ）个.A、9 B、7 C、8 D、6二、填空题
-
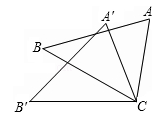
9. 在 ， ， ，0，0.454545…， ， 中，无理数的有个.10. 已知实数x，y满足 +(y+1)2=0，则x+y等于.11. 已知直角三角形的两边长分别为3、4.则第三边长为.12. 把5087精确到百位，这个近似数是.13. 如图，△ACB≌△A′CB′，∠BCB′=30°，则∠ACA′的度数为°.
14. 如图，已知在Rt△ABC中，∠ACB＝90°，AB＝4，分别以AC，BC为直径作半圆，面积分别记为S1 ， S2 ， 则S1＋S2等.
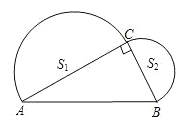15. 在平面直角坐标系中，点P（﹣20，a）与点Q（b，13）关于原点对称，则a+b的值为 ．16. 规定用符号[m]表示一个实数m的整数部分，例如：[ ]=0，[3.14]=3.按此规定，则[ +3]=.17. 如图，有一块直角三角形纸片，两直角边 cm， cm，现将直角边 沿直线 折叠，使它落在斜边 上，且与 重合，则 .
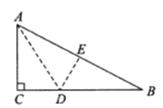18. 如图，在四边形ABCD中，AC平分∠BAD，BC=CD=10，AC=17，AD=9，则AB=.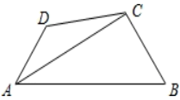
三、解答题
-
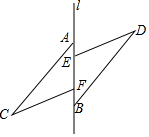
19.(1)、计算：-20190﹣ +(2)、20. 求下列各式中x的值：(1)、4x2-25= 0(2)、1+(x﹣1)3= ﹣7.21. 已知正数x的两个不同的平方根分别为a+3和2a-15，y的立方根是-2，求x-2y+1的值.22. 如图，点A，E，F，B在直线l上，AE=BF，AC∥BD，且AC=BD，求证：CF=DE.
23. 如图，在边长为1个单位长度的小正方形组成的网格中，点A、B、C在小正方形的顶点上.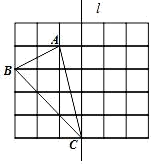
(1)、在图中画出与△ABC关于直线l成轴对称的△A′B′C′.(2)、四边形 ABCA′的面积为；(3)、在直线l上找一点P，使PA+PB的长最短，则这个最短长度为.24. 如图，在四边形ABCD中，∠ABC=∠ADC=90°，连接AC、BD，M、N分别是AC、BD的中点，连接MN
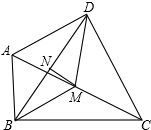(1)、求证：MN⊥BD.(2)、若∠DAC=62°，∠BAC=58°，求∠DMB
