江苏省常州市金坛区2019-2020学年八年级上学期数学12月月考试卷

试卷更新日期：2020-03-04 类型：月考试卷

进入出卷网下载

一、单选题

1. 在 $- \frac{π}{3} ， \sqrt[3]{- \frac{1}{27}} ， \sqrt{8} ， 0.3030030003 ， - \frac{22}{7} ， 3. \overset{\cdot}{1} \overset{\cdot}{4}$ 中，无理数的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 如果 $P (m + 3 ， 2 m + 4)$ 在y轴上，那么点P的坐标是（）

A、 $(- 2 ， 0)$ B、 $(0 ， - 2)$ C、 $(1 ， 0)$ D、 $(0 ， 1)$

查看试题解析
3. 在下列结论中，正确的是（）

A、 $\sqrt{{(- \frac{5}{4})}^{2}} = \pm \frac{5}{4}$ B、x²的算术平方根是x C、﹣x²一定没有平方根 D、 $\sqrt{9}$ 的平方根是 $\pm \sqrt{3}$

查看试题解析
4. 如图所示，数轴上点A所表示的数为 $a$ ，则 $a$ 的值是（）

A、 $\sqrt{5}$ B、 $\sqrt{5} + 1$ C、 $\sqrt{5} - 1$ D、 $- \sqrt{5} + 1$

查看试题解析
5. 已知 $m$ 为非零任意实数，则点 $A (m ， m^{2} + 1)$ 不在（）

A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限

查看试题解析
6. 已知点M(1，a)和点N(2，b)是一次函数y=－2x＋1图象上的两点，则a与b的大小关系是（）

A、a＞b B、a=b C、a＜b D、以上都不对

查看试题解析
7. 已知点(k，b)为第二象限内的点，则一次函数 $y = - k x + b$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
8. 如图，矩形OABC的顶点O与平面直角坐标系的原点重合，点A，C分别在x轴，y轴上，点B的坐标为(－5，4)，点D为边BC上一点，连接OD，若线段OD绕点D顺时针旋转90°后，点O恰好落在AB边上的点E处，则点E的坐标为（）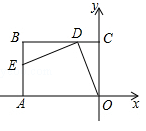

A、(－5，3） B、(－5，4) C、(－5， $\frac{5}{2}$ ） D、(－5，2)

查看试题解析

二、填空题

9. $\sqrt{3}$ -2的相反数是，绝对值是

查看试题解析
10. 如果点 $P (m, 3)$ 与点 $Q (- 5, n)$ 关于 $y$ 轴对称，则 $m + n$ 的值为.

查看试题解析
11. 已知一次函数 $y = k x + 1$ 的图像经过点 $P (- 1, 0)$ ，则 $k =$ .

查看试题解析
12. 关于x的函数y＝（m+1）x﹣（4m﹣3）的图象在第一、二、四象限，那么m的取值范围是.

查看试题解析
13. 已知点M（3，2）与点N（x，y）在同一条平行于x轴的直线上，且点N到y轴的距离为8，则点N的坐标为.

查看试题解析
14. 用四舍五入法对数字1657900精确到千位的结果是.

查看试题解析
15. 如图所示，长方形的长和宽分别为8cm和6cm，剪去一个长为xcm（0＜x＜8）的小长方形（阴影部分）后，余下另个长方形的面积S（cm²）与x（cm）的关系式可表示为.

查看试题解析
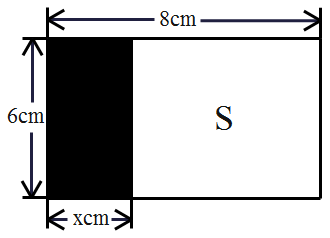16. 某地出租车行驶里程 $x$ （ $k m$ ）与所需费用 $y$ （元）的关系如图.若某乘客一次乘坐出租车里程12 $k m$ ，则该乘客需支付车费元.

查看试题解析
17. 如图，等边三角形的顶点A（1，1）、B（3，1），规定把等边△ABC“先沿x轴翻折，再向左平移1个单位”为一次变换，如果这样连续经过2018次变换后，等边△ABC的顶点C的坐标为.

查看试题解析
18. 在如图的方格中，每个小正方形的边长都为1，△ABC的顶点均在格点上.在建立平面直角坐标系后，点B的坐标为（﹣1，2）.

(1)、①把△ABC向下平移8个单位后得到对应的△A₁B₁C₁ ，画出△A₁B₁C₁；
②画出与△A₁B₁C₁关于y轴对称的△A₂B₂C₂；

(2)、若点P（a，b）是△ABC边上任意一点，P₂是△A₂B₂C₂边上与P对应的点，写出P₂的坐标为；

(3)、试在y轴上找一点Q，使得点Q到B₂、C₂两点的距离之和最小，此时，QB₂+QC₂的最小值为.

查看试题解析

三、解答题

19.

(1)、计算：2018⁰﹣ $\sqrt{4} + \sqrt[3]{- 125}$ ；

(2)、计算： $\sqrt{{(- 2)}^{2}}$ +|1﹣ $\sqrt{2}$ |﹣ ${(\sqrt{2})}^{0}$

查看试题解析
20. 求下列各式中x的值．

(1)、(4x﹣1)²=225

(2)、(x﹣1)³+27=0．

查看试题解析
21. 已知一次函数y₁＝kx+b的图象经过点（0，﹣2），（3，1）.

(1)、求一次函数的表达式，并在所给直角坐标系中画出此函数的图象；

(2)、根据图象回答：当x时，y₁＝0；

(3)、求直线y₁＝kx+b、直线y₂＝﹣2x+4与y轴围成的三角形的面积.

查看试题解析
22. 如图，在平面直角坐标系中，长方形OABC的边OC=2，将过点B的直线y=x﹣3与x轴交于点E．

(1)、求点B的坐标；

(2)、连结CE，求线段CE的长；

(3)、若点P在线段CB上且OP= $\sqrt{11}$ ，求P点坐标．

查看试题解析
23. 已知正比例函数y＝kx经过点A，点A在第四象限，过点A作AH⊥x轴，垂足为点H，点A的横坐标为3，且△AOH的面积为3.

(1)、求正比例函数的表达式；

(2)、在x轴上能否找到一点M，使△AOM是等腰三角形？若存在，求点M的坐标；若不存在，请说明理由.

查看试题解析
24. 在平面直角坐标系中，点A的坐标为（﹣6，6），以A为顶点的∠BAC的两边始终与x轴交于B、C两点（B在C左面），且∠BAC＝45°.

(1)、如图，连接OA，当AB＝AC时，试说明：OA＝OB.

(2)、过点A作AD⊥x轴，垂足为D，当DC＝2时，将∠BAC沿AC所在直线翻折，翻折后边AB交y轴于点M，求点M的坐标.

查看试题解析