浙江省台州市临海市2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-03-04 类型：期末考试

进入出卷网下载

一、选择题（共10小题）

1. 以下四个图形中，其中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若关于x的一元二次方程x²+2x﹣m＝0的一个根是x＝1，则m的值是（）

A、1 B、2 C、3 D、4

查看试题解析
3. 某小组做“用频率估计概率”的试验时，绘出的某一结果出现的频率折线图，则符合这一结果的试验可能是（）

A、抛一枚硬币，出现正面朝上 B、掷一个正六面体的骰子，出现3点朝上 C、任意画一个三角形，其内角和是360° D、从一个装有2个红球1个黑球的袋子中任取一球，取到的是黑球

查看试题解析
4. 如图，PA、PB分别与⊙O相切于A、B两点，点C为⊙O上一点，连AC、BC，若∠P＝80°，则的∠ACB度数为（）

A、40° B、50° C、60° D、80°

查看试题解析
5. 电影《我和我的祖国》讲述了普通人与国家之间息息相关密不可分的动人故事，一上映就获得全国人民的追捧，第一天票房约3亿元，以后每天票房按相同的增长率增长，三天后累计票房收入达10亿元，若把增长率记作x，则方程可以列为（）

A、3（1+x）＝10 B、3（1+x）²＝10 C、3+3（1+x）²＝10 D、3+3（1+x）+3（1+x）²＝10

查看试题解析
6. 用一个半径为15、圆心角为120°的扇形围成一个圆锥，则这个圆锥的底面半径是（）

A、5 B、10 C、5π D、10π

查看试题解析
7. 如图，正比例函数y＝x与反比例函数y＝ $\frac{k}{x}$ 的图象相交于A，C两点．AB⊥x轴于B，CD⊥x轴于D，当四边形ABCD的面积为6时，则k的值是（）

A、6 B、3 C、2 D、 $\frac{3}{2}$

查看试题解析
8. 若抛物线y＝x²+bx+c与x轴只有一个公共点，且过点A（m，n），B（m﹣8，n），则n的值为（）

A、8 B、12 C、15 D、16

查看试题解析
9. 如图，在正方形ABCD中，AB＝5，点M在CD的边上，且DM＝2，△AEM与△ADM关于AM所在的直线对称，将△ADM按顺时针方向绕点A旋转90°得到△ABF，连接EF，则线段EF的长为（）

A、 $\sqrt{34}$ B、 $\sqrt{29}$ C、 $2 \sqrt{7}$ D、 $3 \sqrt{3}$

查看试题解析
10. 已有甲、乙、丙三人，甲说乙在说谎，乙说丙在说谎，丙说甲和乙都在说谎，则（）

A、甲说实话，乙和丙说谎 B、乙说实话，甲和丙说谎 C、丙说实话，甲和乙说谎 D、甲、乙、丙都说谎

查看试题解析

二、填空题（共6小题）

11. 若反比例函数的图象经过点（2，﹣2），（m，1），则m＝．

查看试题解析
12. 如图，在等腰直角△ABC中，∠C＝90°，将△ABC绕顶点A逆时针旋转80°后得到△AB′C′，则∠CAB′的度数为．

查看试题解析
13. 已知（a+b）（a+b﹣4）＝﹣4，那么（a+b）＝．

查看试题解析
14. 某班从三名男生（含小强）和五名女生中，选四名学生参加学校举行的“中华古诗文朗诵大赛”，规定女生选n名，若男生小强参加是必然事件，则n＝．

查看试题解析
15. 如图，已知等边△ABC的边长为4，P是AB边上的一个动点，连接CP，过点P作∠EPC＝60°，交AC于点E，以PE为边作等边△EPD，顶点D在线段PC上，O是△EPD的外心，当点P从点A运动到点B的过程中，点O也随之运动，则点O经过的路径长为．

查看试题解析
16. 扫地机器人能够自主移动并作出反应，是因为它发射红外信号反射回接收器，机器人在打扫房间时，若碰到障碍物则发起警报．若某一房间内A、B两点之间有障碍物，现将A、B两点放置于平面直角坐标系xOy中（如图），已知点A，B的坐标分别为（0，4），（6，4），机器人沿抛物线y＝ax²﹣4ax﹣5a运动．若机器人在运动过程中只触发一次报警，则a的取值范围是．

查看试题解析

三、解答题（共8小题）

17. 已知二次函数y＝2x²+4x+3，当﹣2≤x≤﹣1时，求函数y的最小值和最大值，如图是小明同学的解答过程．你认为他做得正确吗？如果正确，请说明解答依据，如果不正确，请写出你得解答过程．

查看试题解析
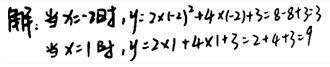18. 某同学报名参加校运动会，有以下5个项目可供选择：径赛项目：100m，200m， $400 m ($ 分别用 $A_{1}$ 、 $A_{2}$ 、 $A_{3}$ 表示 $)$ ；田赛项目：跳远，跳高 $($ 分别用 $B_{1}$ 、 $B_{2}$ 表示 $)$ .

(1)、该同学从5个项目中任选一个，恰好是田赛项目的概率为；

(2)、该同学从5个项目中任选两个，利用树状图或表格列举出所有可能出现的结果，并求恰好是一个田赛项目和一个径赛项目的概率.

查看试题解析
19. 如图，AB、AD是⊙O的弦，△ABC是等腰直角三角形，△ADC≌△AEB，请仅用无刻度直尺作图：

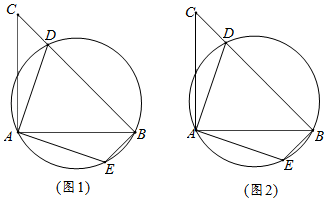(1)、在图1中作出圆心O；

(2)、在图2中过点B作BF∥AC．

查看试题解析
20. “十一”黄金周期间，我市享有“江南八达岭”美誉的江南长城旅游区，为吸引游客组团来此旅游，特推出了如下门票收费标准：
标准一：如果人数不超过20人，门票价格60元/人；

标准二：如果人数超过20人，每超过1人，门票价格降低2元，但门票价格不低于50元/人．

(1)、若某单位组织23名员工去江南长城旅游区旅游，购买门票共需费用多少元？

(2)、若某单位共支付江南长城旅游区门票费用共计1232元，试求该单位这次共有多少名员工去江南长城旅游区旅游？

查看试题解析
21. 如图，AB是⊙O的直径，射线BC交⊙O于点D，E是劣弧AD上一点，且 $\overset{⌢}{A E} = \overset{⌢}{D E}$ ，过点E作EF⊥BC于点F，延长FE和BA的延长线交与点G．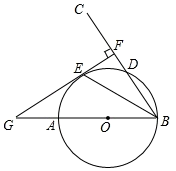

(1)、证明：GF是⊙O的切线；

(2)、若AG＝6，GE＝6 $\sqrt{2}$ ，求⊙O的半径．

查看试题解析
22. 如图1，直线y＝x与双曲线y＝ $\frac{3}{x}$ 交于A，B两点，根据中心对称性可以得知OA＝OB．

(1)、如图2，直线y＝2x+1与双曲线y＝ $\frac{3}{x}$ 交于A，B两点，与坐标轴交点C，D两点，试证明：AC＝BD；

(2)、如图3，直线y＝ax+b与双曲线y＝ $\frac{k}{x}$ 交于A，B两点，与坐标轴交点C，D两点，试问：AC＝BD还成立吗？

(3)、如果直线y＝x+3与双曲线y＝ $\frac{k}{x}$ 交于A，B两点，与坐标轴交点C，D两点，若DB+DC≤5 $\sqrt{2}$ ，求出k的取值范围．

查看试题解析
23. 已知抛物线y＝x²﹣bx+2b（b是常数）．

(1)、无论b取何值，该抛物线都经过定点 D．请写出点D的坐标．

(2)、该抛物线的顶点是（m，n），当b取不同的值时，求n关于m的函数解析式．

(3)、若在0≤x≤4的范围内，至少存在一个x的值，使y＜0，求b的取值范围．

查看试题解析
24. 如图1：在Rt△ABC中，AB＝AC，D为BC边上一点（不与点B，C重合），试探索AD，BD，CD之间满足的等量关系，并证明你的结论．
小明同学的思路是这样的：将线段AD绕点A逆时针旋转90°，得到线段AE，连接EC，DE．继续推理就可以使问题得到解决．

(1)、请根据小明的思路，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论；

(2)、如图2，在Rt△ABC中，AB＝AC，D为△ABC外的一点，且∠ADC＝45°，线段AD，BD，CD之间满足的等量关系又是如何的，请证明你的结论；

(3)、如图3，已知AB是⊙O的直径，点C，D是⊙O上的点，且∠ADC＝45°．
①若AD＝6，BD＝8，求弦CD的长为；

②若AD+BD＝14，求 $A D \cdot (B D + \frac{\sqrt{2}}{2} C D)$ 的最大值，并求出此时⊙O的半径．

查看试题解析