初中数学人教版九年级下学期 第二十八章 28.2 解直角三角形及其应用
试卷更新日期：2020-03-04 类型：同步测试
一、单选题
-
1. 如图所示，河堤横断面迎水坡AB的坡比是1： （坡比是坡面的铅直高度BC与水平宽度AC之比），堤高BC=5m，则坡面AB的长度是（ ）
A、10m B、10 m C、15m D、5 m2. 如图，已知圆内接正三角形的面积为 ，则该圆的内接正六边形的边心距为（ ）
A、2 B、1 C、 D、3. 如图，有一斜坡 ，坡顶B离地面的高度BC为30m，斜坡AB的坡度为1：2，则此斜坡AB为（ ）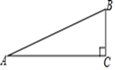
A、 m B、60m C、30m D、15m4. 在边长为1的菱形ABCD中，0°＜∠A＜90°，设∠A＝α，则菱形的面积S与α的函数关系式为（ ）
A、S＝sinα B、S＝cosα C、S＝tanα D、S＝
5. 如图某飞机于空中 处探测到目标 ，此时飞机高度 从飞机上看地平题图面指挥台 的俯角为 ，则飞机 到指挥台 的距离为（ ）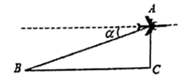
A、 B、 C、 D、二、填空题
-
6. 在Rt△ABC中，∠C=90°，∠A=45°，AC=4，则AB的长是。7. 如图，在矩形ABCD中，DE⊥AC，垂足为E，且tan∠ADE＝ ，AC＝5，则AB的长 ．
8. 如图，在正六边形ABCDEF中，AC＝2 ，则它的边长是 ．
9. 如图，由四个全等的直角三角形围成的大正方形ABCD的面积为34，小正方形EFGH的面积为4，则tan∠DCG的值为.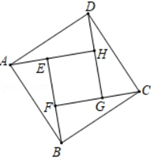
三、综合题
-
10. 如图，湖中的小岛上有一标志性建筑物，其底部为A，某人在岸边的B处测得A在B的北偏东30°的方向上，然后沿岸边直行4公里到达C处，再测得A在C的北偏西45°的方向上(其中A，B，C在同一平面上)．求这个标志性建筑物底部A到岸边BC的最短距离．
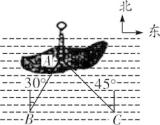11. 如图，男生楼在女生楼的左侧，两楼高度均为90m，楼间距为AB，冬至日正午，太阳光线与水平面所成的角为 ，女生楼在男生楼墙面上的影高为CA；春分日正午，太阳光线与水平面所成的角为 ，女生楼在男生楼墙面上的影高为DA，已知 ．
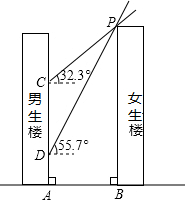(1)、求楼间距AB；(2)、若男生楼共30层，层高均为3m，请通过计算说明多少层以下会受到挡光的影响？ 参考数据： ， ， ， ， ，12. 如图，在Rt△ABC中，∠C=90°，AC=8，sin A=
(1)、求AB的长；(2)、若点E在Rt△ABC的直角边上，点F在斜边AB上，当△CFE∽△ABC时，求CE的长.13. 如图，在电线杆上的点C处引同样长度的拉线CE，CF固定电线杆CD，在离电线杆6米处安置测角仪AB(其中点B、E、D、F在同一条直线上)，在A处测得电线杆上点C处的仰角为30°，测角仪AB的高为 米。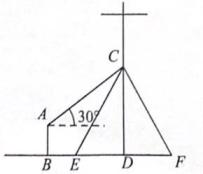
(1)、求电线杆上点C离地面的距离CD(2)、若拉线CE，CF的长度之和为18米，求固定点E和F之间的距离。14. 如图，小明为了测量小河对岸大树BC的高度，他在点A测得大树顶端B的仰角为45°，沿斜坡走3 米到达斜坡上点D，在此处测得树顶端点B的仰角为31°，且斜坡AF的坡比为1：2.
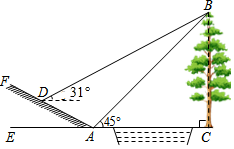(1)、求小明从点A到点D的过程中，他上升的高度；(2)、大树BC的高度约为多少米？（参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）