初中数学人教版九年级下学期 第二十八章 28.1 锐角三角函数
试卷更新日期:2020-03-04 类型:同步测试
一、单选题
-
1. 如图,在Rt△ABC中,∠C=90°,AC=4,AB=5,则sinB的值是( )
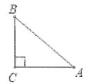 A、 B、 C、 D、2. 如图,把一张长方形纸片ABCD沿对角线BD折叠,使C点落在E处,BE与AD相交于点F,下列结论:①BD=AD2+AB2;②△ABF≌△EDF;③ =
A、 B、 C、 D、2. 如图,把一张长方形纸片ABCD沿对角线BD折叠,使C点落在E处,BE与AD相交于点F,下列结论:①BD=AD2+AB2;②△ABF≌△EDF;③ =④AD=BD•cos45°.其中正确的一组是( )
 A、①② B、②③ C、①④ D、③④3. 如图, AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB= ,BD=5,则OH的长度为( )
A、①② B、②③ C、①④ D、③④3. 如图, AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB= ,BD=5,则OH的长度为( )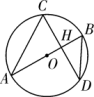 A、 B、 C、1 D、4. 在 中, , , ,则 的值为( )A、 B、 C、 D、5. 已知△ABC中,∠C=90°,若AC= ,BC=1,则sinA的值是( )A、 B、 C、 D、6. 已知:△ABC中,∠BCA=90°,CD⊥AB于D,若AD=1,AB=3,那么 的值是( )
A、 B、 C、1 D、4. 在 中, , , ,则 的值为( )A、 B、 C、 D、5. 已知△ABC中,∠C=90°,若AC= ,BC=1,则sinA的值是( )A、 B、 C、 D、6. 已知:△ABC中,∠BCA=90°,CD⊥AB于D,若AD=1,AB=3,那么 的值是( )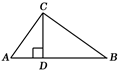 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 计算sin60°tan60°- cos45°cos60°的结果为 。8. 如图,已知直线l1∥l2∥l3∥l4 , 相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα= .
 9. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是边AC的中点,点E,F在边AB上,当△DEF是等腰三角形,且底角的正切值是 时,△DEF腰长的值是 .
9. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是边AC的中点,点E,F在边AB上,当△DEF是等腰三角形,且底角的正切值是 时,△DEF腰长的值是 .
三、计算题
-
10. 2sin60°•tan45°+4cos230°﹣tan60°11. 先化简,再求代数式 ÷(1+ )的值,其中a=3tan30°+1.
四、解答题
-
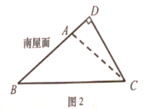
12. 太阳能光伏建筑是太阳能光伏系统与现代绿色环保住宅的完美结合,老刘准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°.求改建后南屋面边沿增加部分AD的长,(结果精确到0.1米)
(参考数据:sin18°≈031,cos18°≈0.95,tan18v≈0.32,sin36°≈0.59)

五、综合题
-
13. 如图,在等腰 中, , , 是 上一点,若 .
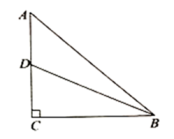 (1)、求 的长;(2)、求 的值.
(1)、求 的长;(2)、求 的值.
-