浙江省宁波市鄞州区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-03-04 类型:期末考试
一、选择题(每小题3分,共30分)
-
1. 下面四个手机APP图标中,可看作轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列命题中,属于真命题的是( )A、两个锐角之和为钝角 B、同位角相等 C、钝角大于它的补角 D、相等的两个角是对顶角3. 点P(2,-3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 为了说明“若a≤b,则ac≤bc”是假命题,c的值可以取( )A、-1 B、0 C、1 D、5. 等腰△ABC中,AB=AC,∠A的平分线交BC于点D,有下列结论:①AD⊥BC;②BD=DC;③∠B=∠C;④∠BAD=∠CAD,其中正确的结论个数是( )A、4个 B、3个 C、2个 D、1个6. 实数a,b,c在数轴上对应的点如图所示,则下列式子一定成立的是( )
2. 下列命题中,属于真命题的是( )A、两个锐角之和为钝角 B、同位角相等 C、钝角大于它的补角 D、相等的两个角是对顶角3. 点P(2,-3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 为了说明“若a≤b,则ac≤bc”是假命题,c的值可以取( )A、-1 B、0 C、1 D、5. 等腰△ABC中,AB=AC,∠A的平分线交BC于点D,有下列结论:①AD⊥BC;②BD=DC;③∠B=∠C;④∠BAD=∠CAD,其中正确的结论个数是( )A、4个 B、3个 C、2个 D、1个6. 实数a,b,c在数轴上对应的点如图所示,则下列式子一定成立的是( )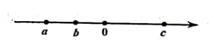 A、a-c>b-c B、ac>bc C、a+c<b+c D、7. 如图,AB=AC,点D,E分别在线段AB,AC上,CD与BE相交于点O,添加以下选项中的一个条件仍不能判定△ABE≌△ACD的是( )
A、a-c>b-c B、ac>bc C、a+c<b+c D、7. 如图,AB=AC,点D,E分别在线段AB,AC上,CD与BE相交于点O,添加以下选项中的一个条件仍不能判定△ABE≌△ACD的是( ) A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD8. 已知AD是△ABC中BC边上的中线,AB=4,AC=6,则AD的取值范围是( )A、2<AD<10 B、1<AD<5 C、4<AD<6 D、4≤AD≤69. 若关于x的不等式 的整数解共有4个,则m的取值范围是( )A、6≤m<7 B、6<m<7 C、6<m≤7 D、6≤m≤710. 第一次“龟兔赛跑”,兔子因为在途中睡觉而输掉比赛,很不服气,决定与乌龟再比一次,并且骄傲地说,这次我一定不睡觉,让乌龟先跑一段距离我再去追都可以赢,结果兔子又一次输掉了比赛,则下列函数图象可以体现这次比赛过程的是( )A、
A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD8. 已知AD是△ABC中BC边上的中线,AB=4,AC=6,则AD的取值范围是( )A、2<AD<10 B、1<AD<5 C、4<AD<6 D、4≤AD≤69. 若关于x的不等式 的整数解共有4个,则m的取值范围是( )A、6≤m<7 B、6<m<7 C、6<m≤7 D、6≤m≤710. 第一次“龟兔赛跑”,兔子因为在途中睡觉而输掉比赛,很不服气,决定与乌龟再比一次,并且骄傲地说,这次我一定不睡觉,让乌龟先跑一段距离我再去追都可以赢,结果兔子又一次输掉了比赛,则下列函数图象可以体现这次比赛过程的是( )A、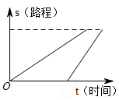 B、
B、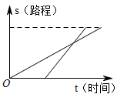 C、
C、 D、
D、
二、填空题(每小题3分,共18分)
-
11. 命题“全等三角形的面积相等”的逆命题是12. 函数y= 的自变量x的取值范围是 。13. 若实数x< ,则x可取的最大整数是。14. 等腰三角形的一个外角等于100°,则它的顶角度数为。15. 如图,D为△ABC外一点,BD⊥AD,BD平分△ABC的一个外角,∠C=∠CAD,若AB=5,BC=3,则BD的长为 。
 16. 如图,R△ABC中,∠C=90°,∠BAC的角平分线AE与AC的中线BD交于点F,P为CE中点,连结PF,若CP=2,S△BFP=15,则AB的长度为。
16. 如图,R△ABC中,∠C=90°,∠BAC的角平分线AE与AC的中线BD交于点F,P为CE中点,连结PF,若CP=2,S△BFP=15,则AB的长度为。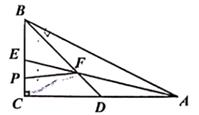
三、解答题(17题—19题每题6分,20题—22题每题8分,23题10分,共52分)
-
17. 解不等式(组)(1)、(2)、18. 如图是由36个边长为1的小正方形拼成的网格图,请按照要求画图:
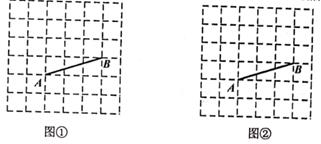 (1)、在图①中画出2个以AB为腰且底边不等的等腰△ABC,要求顶点C是格点;(2)、在图②中画出1个以AB为底边的等腰△ABC,要求顶点C是格点。19. 为提醒人们节约用水,及时修好漏水的水龙头,小明同学做了水龙头漏水实验,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升),已知用于接水的量筒最大容量为100毫升。
(1)、在图①中画出2个以AB为腰且底边不等的等腰△ABC,要求顶点C是格点;(2)、在图②中画出1个以AB为底边的等腰△ABC,要求顶点C是格点。19. 为提醒人们节约用水,及时修好漏水的水龙头,小明同学做了水龙头漏水实验,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升),已知用于接水的量筒最大容量为100毫升。时间t(秒)
10
20
30
40
50
60
70
量筒内水量v(毫升)
4
6
8
10
12
14
16
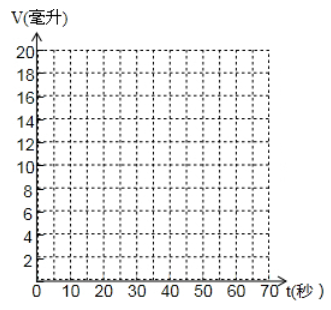 (1)、在图1的平面直角坐标系中,以(t;v)为坐标描出上表中数据对应的点;(2)、用光滑的曲线连接各点,并写出你猜测的ⅴ与t的函数关系式。(3)、解决问题:
(1)、在图1的平面直角坐标系中,以(t;v)为坐标描出上表中数据对应的点;(2)、用光滑的曲线连接各点,并写出你猜测的ⅴ与t的函数关系式。(3)、解决问题:①小明同学所用量筒开始实验前原有存水毫升;
②如果小明同学继续实验,当量筒中的水刚好盛满时所需时间是秒;
③按此漏水速度,半小时会漏水毫升。
20. 如图,在平面直角坐标系中,直线y=-x+m过点A(5,-2)且分别与x轴、y轴交于点B、C,过点A画AD∥x轴,交y轴于点D。 (1)、求点B、C的坐标;(2)、在线段AD上存在点P,使BP+CP最小,求点P的坐标。21. 如图,点C为线段BD上一点,△ABC、△CDE都是等边三角形,AD与CE交于点F,BE与AC相交于点G。
(1)、求点B、C的坐标;(2)、在线段AD上存在点P,使BP+CP最小,求点P的坐标。21. 如图,点C为线段BD上一点,△ABC、△CDE都是等边三角形,AD与CE交于点F,BE与AC相交于点G。 (1)、求证:△ACD≌△BCE;(2)、若CF+CG=8,BD=18,求△ACD的面积。22. 某校八年级举行数学趣味竞赛,购买A,B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元,根据比赛设奖情况,需购买两种笔记本共30本,并且购买A笔记本的数量要少于B笔记本数量的 ,但又不少于B笔记本数量的 。(1)、求A笔记本数量的取值范围;(2)、购买这两种笔记本各多少本时,所需费用最省?最省费用是多少元?23. 定义:如果一个三角形的一个内角等于另一个内角的两倍,则称这样的三角形为“倍角三角形”。
(1)、求证:△ACD≌△BCE;(2)、若CF+CG=8,BD=18,求△ACD的面积。22. 某校八年级举行数学趣味竞赛,购买A,B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元,根据比赛设奖情况,需购买两种笔记本共30本,并且购买A笔记本的数量要少于B笔记本数量的 ,但又不少于B笔记本数量的 。(1)、求A笔记本数量的取值范围;(2)、购买这两种笔记本各多少本时,所需费用最省?最省费用是多少元?23. 定义:如果一个三角形的一个内角等于另一个内角的两倍,则称这样的三角形为“倍角三角形”。 (1)、如图1,△ABC中,AB=AC,∠A为36°,求证:△ABC是倍角三角形;(2)、若△ABC是倍角三角形,∠A>∠B>∠C,∠B=30°,AC=4 ,求△ABC面积:(3)、如图2,△ABC的外角平分线AD与CB的延长线相交于点D,延长CA到点E,使得AE=AB,若AB+AC=BD,请你找出图中的倍角三角形,并进行证明。
(1)、如图1,△ABC中,AB=AC,∠A为36°,求证:△ABC是倍角三角形;(2)、若△ABC是倍角三角形,∠A>∠B>∠C,∠B=30°,AC=4 ,求△ABC面积:(3)、如图2,△ABC的外角平分线AD与CB的延长线相交于点D,延长CA到点E,使得AE=AB,若AB+AC=BD,请你找出图中的倍角三角形,并进行证明。