重庆市南岸区2019届九年级数学中考一模试卷

试卷更新日期：2020-03-04 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣3的相反数是（）

A、 $- \frac{1}{3}$ B、 $\frac{1}{3}$ C、 $- 3$ D、 $3$

查看试题解析
2. （x²y）²的结果是（）

A、x⁶y B、x⁴y² C、x⁵y D、x⁵y²

查看试题解析
3. ${(- π)}^{0}$ 的绝对值是 $($ $)$

A、 $- π$ B、 $π$ C、 $- 1$ D、1

查看试题解析

4. 甲，乙两班举行电脑汉字输入速度比赛，参加学生每分钟输入汉字的个数经统计计算后填人下表：

班级	人数	中位数	方差	平均字数
甲	55	149	191	135
乙	55	151	110	135

某同学根据上表分析得出如下结论：①甲，乙两班学生成绩的平均水平相同；②乙班优秀的人数多于甲班优秀的人数（每分钟输入汉字数≥150个为优秀）；③甲班的成绩的波动情况比乙班的成绩的波动大.上述结论正确的是（）

A、①②③ B、①② C、①③ D、②③

查看试题解析

5. 估计 $\sqrt{7} + 1$ 的值在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
6. 下列命题中的假命题是（）

A、过直线外一点有且只有一条直线与这条直线平行 B、平行于同一直线的两条直线平行 C、直线y＝2x﹣1与直线y＝2x+3一定互相平行 D、如果两个角的两边分别平行，那么这两个角相等

查看试题解析
7. 将一副三角板（∠A＝30°）按如图所示方式摆放，使得AB∥EF，则∠1等于（）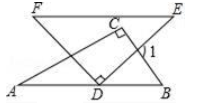

A、75° B、90° C、105° D、115°

查看试题解析
8. 如图所示，在平面直角坐标系中，点A，B，C的坐标分别为（﹣1，3）、（﹣4，1）、（﹣2，1），将△ABC沿一确定方向平移得到△A₁B₁C₁ ，点B的对应点B₁的坐标是（1，2），则点A₁ ， C₁的坐标分别是（）

A、A₁（4，4），C₁（3，2） B、A₁（3，3），C₁（2，1） C、A₁（4，3），C₁（2，3） D、A₁（3，4），C₁（2，2）

查看试题解析
9. 如图，点C在以AB为直径的半圆O的弧上，∠ABC＝30°，且AC＝2，则图中阴影部分的面积是（）

A、 $\frac{4 π}{3}$ ﹣ $\sqrt{3}$ B、 $\frac{4 π}{3}$ ﹣2 $\sqrt{3}$ C、 $\frac{2 π}{3}$ ﹣ $\sqrt{3}$ D、 $\frac{2 π}{3}$ ﹣ $\frac{\sqrt{3}}{2}$

查看试题解析
10. 用棋子摆出下列一组“口”字，按照这种方法摆下去，则第n个“口”字需要用棋子（）

A、（4n﹣4）枚 B、4n枚 C、（4n+4）枚 D、n²枚

查看试题解析
11. 如图，已知四边形OABC是平行四边形，反比例函数y= $\frac{k}{x}$ （k≠0）的图象经过点C，且与AB交于点D，连接OD，CD，若BD=3AD，△OCD的面积是10，则k的值为（）

A、﹣10 B、5 C、 $\frac{8}{3}$ D、 $\frac{16}{3}$

查看试题解析
12. 若数k使关于x的不等式组 ${\begin{array}{l} 3 x + k \leq 0 \\ \frac{x}{3} - \frac{x - 1}{2} \leq 1 \end{array}$ 只有4个整数解，且使关于y的分式方程 $\frac{k}{y - 1}$ +1＝ $\frac{y + k}{y + 1}$ 的解为正数，则符合条件的所有整数k的积为（）

A、2 B、0 C、﹣3 D、﹣6

查看试题解析

二、填空题

13. 将473000用科学记数法表示为．

查看试题解析
14. 把多项式3mx﹣6my分解因式的结果是．

查看试题解析
15. 如图，AB为⊙O的直径，C为圆上（除A、B外）一动点，∠ACB的角平分线交⊙O于D，若AC=8，BC=6，则BD的长为.

查看试题解析
16. 如图，我校初三某班男生期末体考跳远成绩如下折线统计图，则该班男生跳远成绩的中位数是米．

查看试题解析
17. 如图（1）是重庆中国三峡博物馆，又名重庆博物馆，中央地方共建国家级博物馆图（2）是侧面示意图．某校数学兴趣小组的同学要测量三峡博物馆的高GE．如（2），小杰身高为1.6米，小杰在A处测得博物馆楼顶G点的仰角为27°，前进12米到达B处测得博物馆楼顶G点的仰角为39°，斜坡BD的坡i＝1：2.4，BD长度是13米，GE⊥DE，A、B、D、E、G在同一平面内，则博物馆高度GE约为米．（结果精确到1米，参考数据tan27°≈0.50，tan39°≈0.80）

查看试题解析
18. 一辆快车从甲地开往乙地，一辆慢车从乙地开往甲地，两车同时出发，设快车离乙地的距离为y₁（km），慢车离乙地的距离为y₂（km），慢车行驶时间为x（h），两车之间的距离为s（km）．y₁ ， y₂与x的函数关系图象如图1所示，s与x的函数关系图象如图2所示．则下列判断：①图1中a＝3；②当x＝ $\frac{15}{8}$ h时，两车相遇；③当x＝ $\frac{3}{2}$ 时，两车相距60km；④图2中C点坐标为（3，180）；⑤当x＝ $\frac{5}{8}$ h或 $\frac{25}{8}$ h时，两车相距200km．其中正确的有（请写出所有正确判断的序号）

查看试题解析

三、解答题

19. 如图，直线 AB∥CD，直线 EF 与 AB 相交于点 P，与 CD 相交于点 Q，且 PM⊥EF，若∠1=68°，求∠2 的度数．

查看试题解析
20. 某中学为推动“时刻听党话永远跟党走”校园主题教育活动，计划开展四项活动：A：党史演讲比赛，B：党史手抄报比赛，C：党史知识竞赛，D：红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查，随机抽取了部分学生，并将调查结果绘制成图1，图2两幅不完整的统计图.请结合图中信息解答下列问题：

(1)、本次共调查了名学生；

(2)、将图1的统计图补充完整；

(3)、已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生，现从这4名学生中任意抽取2名学生参加该项目比赛，请用画树状图或列表的方法，求出恰好抽到一名男生一名女生的概率.

查看试题解析
21. 计算：

(1)、 $a (a + 2 b) - (a + b) (a - b)$

(2)、 $(\frac{x + 2}{x - 3} + x + 2) \div \frac{x^{2} - 4 x + 4}{x - 3}$

查看试题解析
22. 如图，在矩形ABCD中，AB＝2，BC＝3，M是BC的中点，DE⊥AM于点E．

(1)、求证：△ADE∽△MAB；

(2)、求DE的长．

查看试题解析
23. 夏日来临，为了保证顾客每天都能吃到新鲜水果，“每日鲜果”水果店要求当日批发购进的某水果当夭必须全部售出．该水果购进的价格为5元/千克．经调查发现，当销售单价为10元/千克时，销售量为200千克；销售单价每上涨1元/千克，销售量就会减少40千克．

(1)、若每天至少卖出120千克，销售单价最高定为多少？

(2)、某天“每日鲜果”水果店按（1）中最高售价的方案进货，以（1）中的最高售价销售了3a千克的水果后，店内保鲜及冷凝系统发生故障，导致剩下水果中的a%变质而无法销售．店长马上决定将剩余可销售的水果立刻榨汁，并分装保鲜瓶中（每瓶能装果汁0.5千克）售卖，随后果汁被一抢而空．已知此水果的出汁率为40%（即1千克水果可榨出0.4千克果汁），每瓶果汁售价为10元．若当天销售完毕后水果店因销售此水果获得的总利润为648元．求a的值．

查看试题解析
24. 如图在等腰△ABC中，AB＝AC＝20cm，BC＝16cm，AD＝BD．

(1)、点M在底边BC上且以6cm/s的速度由B点向C点运动，同时，点N在腰AC上且由C点向A点运动．
①如果点M与点N的运动速度相等，求经过多少秒后△BMD≌△CNM；

②如果点M与点N的运动速度不相等，当点N的运动速度为多少时，能够使△BMD与△CNM全等？

(2)、如果点N以②中的运动速度从点C出发，点M以6cm/s的速度从点B同时出发，都逆时针沿△ABC三边运动，直接写出当点M与点N第一次相遇时点M运动的路程．

查看试题解析
25. 如果一个正整数m能写成m＝a²﹣b²（a、b均为正整数，且a≠b），我们称这个数为“平方差数”，则a、b为m的一个平方差分解，规定：F（m）＝ $\frac{b}{a}$ ．
例如：8＝8×1＝4×2，由8＝a²﹣b²＝（a+b）（a﹣b），可得 ${\begin{array}{l} a + b = 8 \\ a - b = 1 \end{array}$ 或 ${\begin{array}{l} a + b = 4 \\ a - b = 2 \end{array}$ ．因为a、b为正整数，解得 ${\begin{array}{l} a = 3 \\ b = 1 \end{array}$ ，所以F（8）＝ $\frac{1}{3}$ ．又例如：48＝13²﹣11²＝8²﹣4²＝7²﹣1² ，所以F（48）＝ $\frac{11}{13}$ 或 $\frac{1}{2}$ 或 $\frac{1}{7}$ ．

(1)、判断：6平方差数（填“是“或“不是“），并求F（45）的值；

(2)、若s是一个三位数，t是一个两位数，s＝100x+5，t＝10y+x（1≤x≤4，1≤y≤9，x、y是整数），且满足s+t是11的倍数，求F（t）的最大值．

查看试题解析
26. 如图①，抛物线y＝﹣ $\frac{1}{2}$ x²+x+4与x轴交于A，B两点，与y轴交于点C，点D为线段AC的中点，直线BD与抛物线交于另一点E，与y轴交于点F．

(1)、求直线BD的解析式；

(2)、如图②，点P是直线BE上方抛物线上一动点，连接PD，PF，当△PDF的面积最大时，在线段BE上找一点G，使得PG﹣ $\frac{\sqrt{5}}{5}$ GE的值最小，求出点G的坐标及PG﹣ $\frac{\sqrt{5}}{5}$ GE的最小值；

(3)、将抛物线沿直线AC平移，点A，C平移后的对应点为A′，C'．在平面内有一动点H，当以点B，A'，C'，H为顶点的四边形为平行四边形时，在直线AC上方找一个满足条件的点H，与直线AC下方所有满足条件的点H为顶点的多边形为轴对称图形时，求出点A′的坐标．

查看试题解析