重庆市东岸区2019届九年级数学中考一模试卷

试卷更新日期：2020-03-04 类型：中考模拟

进入出卷网下载

一、单选题

1. 写出π﹣3.14的相反数是（）

A、3.14﹣π B、0 C、π+31.4 D、﹣π﹣3.14

查看试题解析
2. 下列计算中，不正确的有（）
①（ab²）³=ab⁶；②（3xy²）³=9x³y⁶；③（﹣2x³）²=﹣4x⁶；④（﹣a^2m）³=a^6m ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 计算|﹣3|﹣2018⁰的结果是（）

A、﹣2021 B、﹣2015 C、﹣4 D、2

查看试题解析
4. 下列说法不正确的是（）

A、数据0、1、2、3、4、5的平均数是3 B、选举中，人们通常最关心的数据是众数 C、数据3、5、4、1、2的中位数是3 D、甲、乙两组数据的平均数相同，方差分别是S_甲²=0.1，S_乙²=0.11，则甲组数据比乙组数据更稳定

查看试题解析
5. 已知a为整数，且 $\sqrt{3} < a < \sqrt{5}$ ，则a等于（）

A、1 B、2 C、3 D、4

查看试题解析
6. 给出下列命题： $①$ 两边及一边上的中线对应相等的两个三角形全等； $②$ 底边和顶角对应相等的两个等腰三角形全等； $③$ 斜边和斜边上的高线对应相等的两个直角三角形全等，其中属于真命题的是（）

A、 $① ②$ B、 $② ③$ C、 $① ③$ D、 $① ② ③$

查看试题解析
7. 一副直角三角板如图放置，其中∠C＝∠DFE＝90°，∠A＝45°，∠E＝60°，点F在CB的延长线上.若DE∥CF，则∠BDF等于（　　）

A、35° B、30° C、25° D、15°

查看试题解析
8. 若将点A（1，3）向左平移2个单位，再向下平移4个单位得到点B，则点B的坐标为（）

A、（﹣2，0） B、（﹣2，﹣1） C、（﹣1，﹣1） D、（﹣1，0）

查看试题解析
9. 如图，已知AB是⊙O的直径，点C在⊙O上，∠CAB＝30°，AC＝3 $\sqrt{3}$ ，则图中阴影部分的面积是（）

A、 $\frac{3}{2} π - \frac{9}{4} \sqrt{3}$ B、 $\frac{3}{2} π$ C、 $\frac{3}{2} π - \frac{9}{4}$ D、 $3 π - \frac{9}{4} \sqrt{3}$

查看试题解析
10. 如图所示，第1个图案是由黑白两种颜色的六边形地面砖组成的，第2个，第3个图案可以看成是由第1个图案经过平移而得，那么第n个图案中有白色六边形地面砖（）块．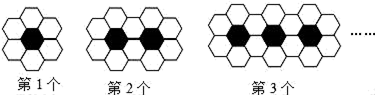

A、6+4（n+1） B、6+4n C、4n﹣2 D、4n+2

查看试题解析
11. 如图，平行四边形ABCD中，点A在反比例函数y= $\frac{k}{x}$ （k≠0）的图象上，点D在y轴上，点B、点C在x轴上．若平行四边形ABCD的面积为10，则k的值是（）

A、﹣10 B、﹣5 C、5 D、10

查看试题解析
12. 使得关于x的不等式组 ${\begin{array}{l} 6 x - a \geq - 10 \\ - 1 + \frac{1}{2} x < - \frac{1}{8} x + \frac{3}{2} \end{array}$ 有且只有4个整数解，且关于x的分式方程 $\frac{a x - 1}{4 - x}$ + $\frac{27}{x - 4}$ =-8的解为正数的所有整数a的值之和为（）

A、11 B、15 C、18 D、19

查看试题解析

二、填空题

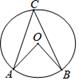
13. 将201800000用科学记数法表示为．

查看试题解析
14. 因式分解：2x²﹣4x═ ．

查看试题解析
15. 如图，在⊙O中，C为优弧AB上一点，若∠ACB＝40°，则∠AOB＝度．

查看试题解析
16. 国家科学技术进步奖是国务院设立的国家科学技术奖五大奖项之一，根据国家统计局公布的奖项数绘制成折线统计图，则奖项数的中位数为．

查看试题解析
17. 如图，已知点C与某建筑物底端B相距306米（点C与点B在同一水平面上），某同学从点C出发，沿同一剖面的斜坡CD行走195米至坡顶D处，斜坡CD的坡度（或坡比）i＝1：2.4，在D处测得该建筑物顶端A的俯视角为20°，则建筑物AB的高度约为（精确到0.1米，参考数据：sin20°≈0.342，cos20°≈0.940，tan20°≈0364）．

查看试题解析
18. 一辆快车从甲地开往乙地，一辆慢车从乙地开往甲地，两车同时出发，设快车离乙地的距离为y₁（km），慢车离乙地的距离为y₂（km），慢车行驶时间为x（h），两车之间的距离为s（km）．y₁ ， y₂与x的函数关系图象如图1所示，s与x的函数关系图象如图2所示．则下列判断：①图1中a＝3；②当x＝ $\frac{15}{8}$ h时，两车相遇；③当x＝ $\frac{3}{2}$ 时，两车相距60km；④图2中C点坐标为（3，180）；⑤当x＝ $\frac{5}{8}$ h或 $\frac{25}{8}$ h时，两车相距200km．其中正确的有（请写出所有正确判断的序号）

查看试题解析

三、解答题

19. 如图，AB∥CD，点E、G分别是AB、CD上的点，且∠AEG＝34°，EF⊥EG交CD于点F，求∠EFG的度数．

查看试题解析
20. 国家为了实现2020年全面脱贫目标，实施“精准扶贫”战略，采取易地搬迁，产业扶持等措施．使贫困户的生活条件得到改善，生活质量明显提高．某旗县为了全面了解贫困县对扶贫工作的满意度情况，进行随机抽样调查，分为四个类别：A．非常满意；B．满意；C．基本满意；D．不满意．依据调查数据绘制成图1和图2的统计图（不完整）．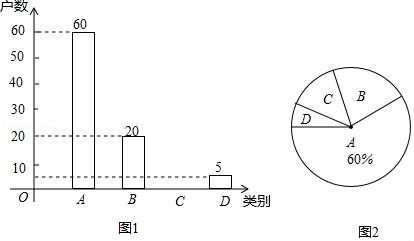

根据以上信息，解答下列问题：

(1)、将图1补充完整；

(2)、通过分析，贫困户对扶贫工作的满意度（A、B、C类视为满意）是；

(3)、市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中，随机抽取两户进行满意度回访，求这两户贫困户恰好都是同一乡镇的概率．

查看试题解析
21. 计算：

(1)、（a+b）（a﹣b）+a（3b﹣a）；

(2)、（1﹣x+ $\frac{1 - 2 x}{x - 1}$ ） $\div \frac{x}{x^{2} - 2 x + 1}$ ．

查看试题解析
22. 如图，已知矩形 ABCD 中，AB＝1，BC＝ $\sqrt{3}$ ，点 M 在 AC 上，且 AM＝ $\frac{1}{4}$ AC，连接并延长 BM 交 AD 于点 N．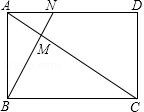

(1)、求证：△ABC∽△AMB；

(2)、求 MN 的长．

查看试题解析
23. “饺子“又名“交子”或者“娇耳”，是新旧交替之意，它是重庆人民的年夜饭必吃的一道美食．今年除夕，小侨跟着妈妈一起包饺子准备年夜饭，体验浓浓的团圆气氛．已知小侨家共10人，平均每人吃10个饺子，计划用10分钟将饺子包完．

(1)、若妈妈每分钟包饺子的速度是小侨速度的2倍少2个，那么小侨每分钟至少要包多少个饺子？

(2)、小侨以（1）问中的最低速度，和妈妈同时开始包饺子，妈妈包饺子的速度在（1）问的最低速度基础上提升了 $\frac{5}{4}$ a%，在包饺子的过程中小侨外出耽误了 $\frac{a}{40}$ 分钟，返家后，小侨与妈妈一起包完剩下的饺子，所用时间比原计划少了 $\frac{1}{2}$ a%，求a的值．

查看试题解析
24. 如图，在△ABC中，AB＝AC，点D、E在线段BC上，且BE＝CD，连接AD、AE，过点D作DF⊥AE，垂足为H，交AC于点F，过点E作EG⊥AC，垂足为G．

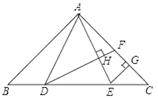(1)、若DH＝4，AD＝5，HF＝1，求AF的长；

(2)、若∠BAC＝90°，求证：AF＝2CG．

查看试题解析
25. 如图，在一块边长为a米的正方形空地的四角均留出一块边长为b（b＜ $\frac{a}{2}$ ）米的正方形修建花坛，其余的地方种植草坪．

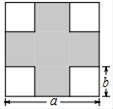(1)、用代数式表示草坪的面积；

(2)、先对上述代数式进行因式分解再计算当a＝15，b＝2.5时草坪的面积．

查看试题解析
26. 如图，平面直角坐标系中，O为坐标原点，直线y＝﹣ $\frac{1}{2}$ x+4交x轴于点C，交y轴于点A，过A、C两点的抛物线y＝ax²+bx+4交x轴负半轴于点B，且tan∠BAO＝ $\frac{3}{4}$ ．

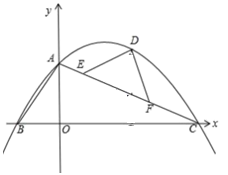(1)、求抛物线的解析式；

(2)、已知E、F是线段AC上异于A、C的两个点，且AE＜AF，EF＝2 $\sqrt{5}$ ，D为抛物线上第一象限内一点，且DE＝DF，设点D的横坐标为m，△DEF的面积为S，求S与m的函数关系式（不要求写出自变量m的取值范围）；

(3)、在（2）的条件下，当∠EDF＝90°时，连接BD，P为抛物线上一动点，过P作PQ⊥BD交线段BD于点Q，连接EQ．设点P的横坐标为t，求t为何值时，PE＝QE．

查看试题解析