辽宁省沈阳市和平区2019届九年级数学中考一模试卷
试卷更新日期:2020-03-04 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、2 B、 C、 D、2. 如图是一个正方体纸盒的展开图,每个面上都标注了字母或数字,在正方体展开前,标注a的面的对面上所标注的数字是( )
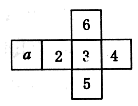 A、3 B、4 C、5 D、63. 如图, , 于点C, 的延长线与 交于点E,若 ,则 等于( )
A、3 B、4 C、5 D、63. 如图, , 于点C, 的延长线与 交于点E,若 ,则 等于( ) A、 B、 C、 D、4. 在一个暗箱里放有a个除颜色外其它完全相同的球,这a个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是( )A、12 B、9 C、4 D、35. 把不等式组 的解集表示在数轴上,如下图,正确的是( )A、
A、 B、 C、 D、4. 在一个暗箱里放有a个除颜色外其它完全相同的球,这a个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是( )A、12 B、9 C、4 D、35. 把不等式组 的解集表示在数轴上,如下图,正确的是( )A、 B、
B、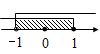 C、
C、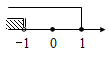 D、
D、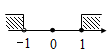 6. 下列运算中,正确的是( )A、 B、 C、 D、7. 关于x的一元二次方程 根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定8. 某班体育委员统计了全班45名同学一周的体育锻炼时间(单位:小时),并绘制了如图所示的折线统计图,下列说法中错误的是( )
6. 下列运算中,正确的是( )A、 B、 C、 D、7. 关于x的一元二次方程 根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定8. 某班体育委员统计了全班45名同学一周的体育锻炼时间(单位:小时),并绘制了如图所示的折线统计图,下列说法中错误的是( )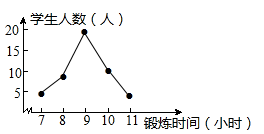 A、众数是9小时 B、中位数是9小时 C、平均数是9小时 D、锻炼时间不低于9小时的有14人9. 已知三点 , , 都在反比例函数 的图象上,若 , ,则下列式子正确的是( )A、 B、 C、 D、10. 某市在旧城改造过程中,需要整修一段全长2400m的道路.为了尽量减少施工对城市交通所造成的影响,实际工作效率比原计划提高了20%,结果提前8小时完成任务.求原计划每小时修路的长度.若设原计划每小时修路xm,则根据题意可得方程( )A、 B、 C、 D、
A、众数是9小时 B、中位数是9小时 C、平均数是9小时 D、锻炼时间不低于9小时的有14人9. 已知三点 , , 都在反比例函数 的图象上,若 , ,则下列式子正确的是( )A、 B、 C、 D、10. 某市在旧城改造过程中,需要整修一段全长2400m的道路.为了尽量减少施工对城市交通所造成的影响,实际工作效率比原计划提高了20%,结果提前8小时完成任务.求原计划每小时修路的长度.若设原计划每小时修路xm,则根据题意可得方程( )A、 B、 C、 D、二、填空题
-
11. 分解因式: .12. 长城的总长大约为6700000m,将数6700000用科学记数法表示为13. 用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n个图形需要棋子枚.
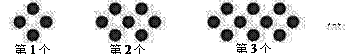 14. 如图,在菱形 中,E是 上一点, 的延长线交 于点F,若 ,则 的度数为.
14. 如图,在菱形 中,E是 上一点, 的延长线交 于点F,若 ,则 的度数为.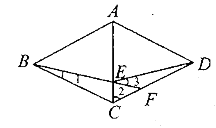 15. 的半径为1, ,将射线 绕点P旋转 度( )得到射线 ,若直线 恰好与 相切,则 的值为.16. 如图,矩形ABCD中,由8个面积均为1的小正方形组成的L型模板如图放置,则矩形ABCD的面积为 .
15. 的半径为1, ,将射线 绕点P旋转 度( )得到射线 ,若直线 恰好与 相切,则 的值为.16. 如图,矩形ABCD中,由8个面积均为1的小正方形组成的L型模板如图放置,则矩形ABCD的面积为 .
三、解答题
-
17. 计算:18. 将分别标有数字1,2,3的三张卡片(卡片除所标注数字外其他均相同)洗匀后,背面朝上放在桌面上.(1)、随机地抽取一张,直接写出抽到的卡片所标数字是奇数的概率;(2)、随机地抽取一张,将卡片上标有的数字作为十位上的数字(不放回),再随机地抽取一张卡片,将卡片上标有的数字作为个位上的数字,用列表或树状图的方法求组成的两位数恰好是“32”的概率.19. 如图,在 中, 分别平分 和 ,交 于点 ,线段 相交于点M.
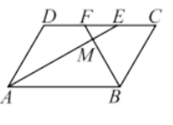 (1)、求证: ;(2)、若 ,则 的值是.20. 为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
(1)、求证: ;(2)、若 ,则 的值是.20. 为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.种类
A
B
C
D
E
出行方式
共享单车
步行
公交车
的士
私家车
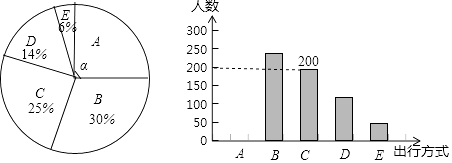
根据以上信息,回答下列问题:
(1)、参与本次问卷调查的市民共有人,其中选择B类的人数有人;(2)、在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;(3)、该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.21. 如图,某中心广场灯柱AB被钢缆CD固定,已知CB=5米,且sin∠DCB= .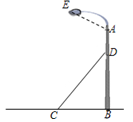 (1)、求钢缆CD的长度。(2)、若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?22. 如图,在 中, ,以 为直径的 交 于点D,E为 的中点,连接 .
(1)、求钢缆CD的长度。(2)、若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?22. 如图,在 中, ,以 为直径的 交 于点D,E为 的中点,连接 .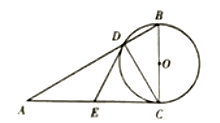 (1)、求证: 是 的切线;(2)、若 ,求 的长.23. 国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元.种粮大户老王今年种了150亩地,计划明年再承租50~150亩土地种粮以增加收入,考虑各种因素,预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系如图所示.
(1)、求证: 是 的切线;(2)、若 ,求 的长.23. 国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元.种粮大户老王今年种了150亩地,计划明年再承租50~150亩土地种粮以增加收入,考虑各种因素,预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系如图所示.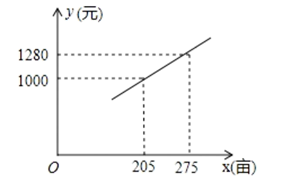 (1)、今年老王种粮可获得补贴元;(2)、求y与x之间的函数关系式;(3)、若老王明年每亩的售粮收入能达到2100元,设老王明年种粮利润为w(元).(种粮利润=售粮收入-种粮成本+种粮补贴)
(1)、今年老王种粮可获得补贴元;(2)、求y与x之间的函数关系式;(3)、若老王明年每亩的售粮收入能达到2100元,设老王明年种粮利润为w(元).(种粮利润=售粮收入-种粮成本+种粮补贴)①求老王明年种粮利润w(元)与种粮面积x(亩)之间的函数关系式;
②当种粮面积为多少亩时,老王明年种粮利润最高?
24. 如图1,在正方形ABCD中,AD=6,点P是对角线BD上任意一点,连接PA,PC过点P作PE⊥PC交直线AB于E.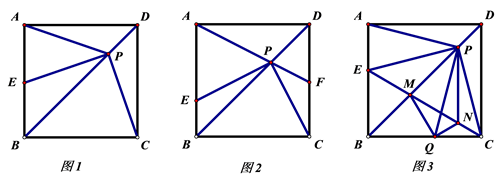 (1)、求证:PC=PE;(2)、延长AP交直线CD于点F.
(1)、求证:PC=PE;(2)、延长AP交直线CD于点F.①如图2,若点F是CD的中点,求△APE的面积;
②若ΔAPE的面积是 ,则DF的长为
(3)、如图3,点E在边AB上,连接EC交BD于点M,作点E关于BD的对称点Q,连接PQ,MQ,过点P作PN∥CD交EC于点N,连接QN,若PQ=5,MN= ,则△MNQ的面积是25. 如图1,抛物线 与x轴,y轴的正半轴分别交于点 和点 ,与x轴负半轴交于点A,动点M从点A出发沿折线 向终点B匀速运动,将线段 绕点O顺时针旋转 得到线段 ,连接 . (1)、求抛物线 的函数表达式;(2)、如图2,当点N在线段 上时,求证: ;(3)、当点N在线段 上时,直接写出此时直线 与抛物线交点的纵坐标;(4)、设 的长度为n,直接写出在点M移动的过程中, 的取值范围.
(1)、求抛物线 的函数表达式;(2)、如图2,当点N在线段 上时,求证: ;(3)、当点N在线段 上时,直接写出此时直线 与抛物线交点的纵坐标;(4)、设 的长度为n,直接写出在点M移动的过程中, 的取值范围.