浙江省宁波市2019-2020学年数学中考模拟试卷
试卷更新日期：2020-03-04 类型：中考模拟
一、仔细选一选（本题共 12小题，每题 4分，共48分）
-
1. -3的绝对值是（ ）A、3 B、 C、-3 D、-2. 宁波市去年实现地区生产总值约为10745.5亿元，其中10475.5亿用科学记数法表示为（ ）A、
B、
C、
D、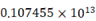
3. 下列计算正确的是（ ）A、
B、
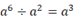C、
D、（a2）3=a6
4. 从长为10cm,7cm,5cm,3cm的四条线段中，任取三条能够组成三角形的概率是（ ）A、 B、 C、 D、5. 已知：如图，是由若干个大小相同的小正方体所搭成的几何体的三视图，则搭成这个几何体的小正方体的个数是（ ）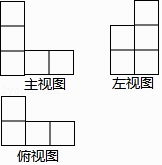
A、6个 B、7个 C、8个 D、9个6. 如图是宁波市某周内最高气温的折线统计图，关于这7天的日最高气温的说法正确的是（ ）
A、极差是6 B、众数是9 C、中位数是8 D、平均数是97. 若正多边形的一个外角是60°，那么该正多边形的内角和为（ ）A、180° B、360° C、540° D、720°8. 如图，EF过▱ABCD对角线的交点O交AD于点E，交BC于点F，若▱ABCD的周长为18，OE=1.5，则四边形EFCD的周长为（ ）
A、14 B、13 C、12 D、109. 如图，在Rt△ABC中，∠ACB=90°，AC=BC=1，将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE，点B经过的路线为弧BD，则图中阴影部分的面积是（ ）
A、 B、 C、 D、10. 如图，双曲线y= (ｘ＞0 )经过四边形OABC的顶点A和C，∠ABC=90°，OC平分OA与x轴正半轴的夹角，AB∥x轴，将△ABC沿AC翻折后得△AB'C，点B'落在OA上，则△ABC的面积是（ ）
A、 B、 C、 D、311. 如图，有一个长方形ABCD，过点G、H分别作AB的平行线，过点E作AD的平行线，AG=BE，GH=AE，将整个矩形分成了①②③④⑤⑥这六部分，连结BP和PD，请问已知△BPD的面积，则能求出哪部分面积（ ）
A、③ B、④ C、⑤ D、⑥12. 如图，在平面直角坐标系中，已知在矩形ABCD中，AB=2，BC=1，点A从点O开始沿x轴正方向移动，点B在第一象限的角平分线上，求点C到原点O的最大距离（ ）
A、
B、3
C、
D、4
二、认真填一填（共6题，每题4分，共24分）
-
13. 因式分解：
= ； 14. 一个正数的平方根是x+1和x-3，则x= ；15. 要使分式 的值为0，x的取值为 ；
16. 如图，一艘轮船在A处测得灯塔P位于其北偏东60°方向上，轮船沿正东方向航行30海里到达B处后，此时测得灯塔P位于其北偏东30°方向上，此时轮船与灯塔P的距离是 ；
17. 如图，矩形OABC的对角线OB长为6，顶点A，C在坐标轴上，反比例函数
（k>0，x>0）的图象交边BC于点E，交边AB于点D，连结DE，若CE=2BE，则DE的长为 ； 
18. 如图，已知半圆O的直径AB=4，沿它的一条弦折叠，若折叠后得圆弧与直径AB相切于点D，且AD：BD=3：1，则折痕EF的长为 ；
三、全面解一解（共8个小题，共78 分，各小题都必须写出解答过程）
-
19. 先化简，再求值 ,其中x选取一个合适的数进行求值
20. 在5×3的方格纸中，线段AB的两个端点都在格点上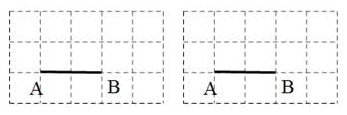
(1)、图1中画一个以AB为边的△ABC，使△ABC是一个面积为2的轴对称图形，其中C为格点(2)、图2中画一个以AB为边的四边形ABCD，使四边形ABCD是中心对称图形，且C，D为格点21. 外出旅游已是现中国很多家庭在春节期间所选择的休闲方式之一，游客的年龄结构呈年轻化发展，下图是经问卷调查得到的今年春节旅游消费人群年龄分布类别
A
B
C
D
E
年龄
25以下
25-34
35-44
45-54
55及以上
根据以上信息，回答下列问题：
(1)、参与本次问卷调查的共有人，其中选择B类的有人(2)、在扇形统计图中，求A类对应扇形圆心角的度数，并补全条形统计图(3)、若宁波市约有400万人春节期间外出旅游，那么请估计35岁以下的人数22. 已知抛物线
与两坐标轴分别交于A(-1，0)，C(0，-3)，一次函数的图象与抛物线交于B，C两点
(1)、求二次函数的解析式(2)、请求出一次函数的解析式并结合图象，直接写出当一次函数值小于二次函数时自变量x的取值范围23. 如图，四边形ABCD与四边形AEFG都是菱形，其中点C在AF上，点E、G分别在BC、CD上。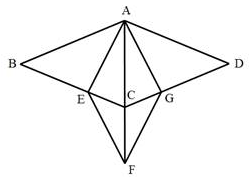
(1)、求证：△ABE≌△ADG(2)、若∠BAD=135°，∠EAG=75°，求AB与AE的比24. 做服装生意的王老板经营甲、乙两个店铺，每个店铺在同一段时间内都能售出A、B两种款式的服装合计30件，并且每售出一件A款式和B款式服装，甲店铺获利分别为30元和35元，乙店铺利润分别为26元和36元。某日王老板进A款式服装36件，B款式服装24件，并将这批服装分配给两个店铺各30件(1)、怎样将这60件服装分配给甲、乙两个店铺，能使两个店铺在销售完这批服装后所获利润相同？(2)、怎样分配这60件服装能保证在甲店铺获利不少于950元的前提下，王老板获利最大？最大总利润是多少？25. 数学上称“费马点”是位于三角形内且到三角形三个顶点距离之和最短的点。现定义：菱形对角线上一点到该对角线同侧两条边上的两点距离最小的点称为类费马点。
例如：菱形ABCD，P是对角线BD上一点，E、F是边BC和CD上的两点，若点P满足PE与PF之和最小，则称点P为类费马点
(1)、如图1，在菱形ABCD中，AB=4，点P是BD上的类费马点①E为BC的中点，F为CD的中点，则PE+PF=。
②E为BC上一动点，F为CD上一动点，且∠ABC=60°则PE+PF=。
(2)、如图2，在菱形ABCD中，AB=4，连结AC，点P是△ABC的费马点，（即PA，PB，PC之和最小），①当∠ABC=60°时，BP=▲②当∠ABC=30°时，你能找到△ABC的费马点P吗？画图做简要说明，并求此时PA+PB+PC的值
26. 如图1，直线l：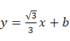
与x轴、y轴分别交于点A，B，点C 
在直线l上，点P的坐标为（0，2），以点P为圆心，PC长为半径画⊙P. 
(1)、求直线l的解析式(2)、求∠BAO的度数(3)、判断直线l与⊙P的位置关系，并证明你的结论(4)、如图2，点M(m，0)，N(n，0)是x轴上的两个动点（点M在点N的左侧），且
，直线CM，CN与⊙P分别交于D，E，直线DE与x轴交于点Q，试探索∠DQM的大小是否变化，请说明理由。 