浙江省湖州市吴兴区2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2020-03-04 类型：期末考试

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分）

1. -3的倒数是（）

A、3 B、 $- \frac{1}{3}$ C、 $\frac{1}{3}$ D、1

查看试题解析
2. 中国人很早就开始使用了负数，中国古代数学著作《九章算术》就有记载．如果收入100元记作+100元．那么−80元表示（）

A、支出20元 B、收入20元 C、支出80元 D、收入80元

查看试题解析
3. 下列四个运算中，结果最大的是（）

A、1-（-2） B、1+（-2） C、1×（-2） D、1÷（-2）

查看试题解析
4. 吴兴区自2003年成立以来，本着“生态吴兴、经济强区、科技新城、幸福家园”的总战略，全区的经济实力显著增强。2018年，全区实现年财政总收入146.59亿元，将146.59亿用科学记数法表示正确的是（）

A、1.4659×10⁷ B、1.4659×10⁹ C、146.59×10⁸ D、1.4659×10¹⁰

查看试题解析
5. 估计 $\sqrt{11} + 2$ 的值在（）

A、3到4之间 B、4到5之间 C、5到6之间 D、6到7之间

查看试题解析
6. 如图，三条直线a、b、c相交于一点，则∠1+∠2+∠3＝（）

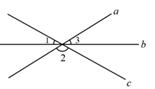A、360° B、180° C、120° D、90°

查看试题解析
7. 下列选项中，正确的是（）

A、若a²=b² ，则a=b B、 $- （ - 1 ）^{2018} = - 1$ C、2a+3b=5ab D、一个数的绝对值一定是正数

查看试题解析
8. 如图，AC⊥BC，AC=4，点D是线段BC上的动点，则A，D两点之间的距离不可能是（）

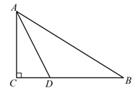A、3.5 B、4.5 C、5 D、5.5

查看试题解析
9. 代数式2ax+5b的值会随x的取值不同而不同，下表是当x取不同值时对应的代数式的值，则关于x的方程2ax+5b=-4的解是（）

x

-4

-3

-2

-1

0

2ax+5b

12

8

4

0

-4

A、12 B、4 C、-2 D、0

查看试题解析
10. “幻方”最早记载于春秋时期的《大戴礼》中，现将1、2、3、4、5、7、8、9这8个数字填入如图1所示的“幻方”中，使得每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等．现有如图2所示的“幻方”，则（x-y）^m-n的值是（）

A、-27 B、-1 C、8 D、16

查看试题解析

二、填空题（共6小题，每小题4分，共24分）

11. 代数式 $\frac{5}{2} x y^{2}$ 的系数是．

查看试题解析
12. 比较大小： $- | - 5 |$ $- (- 4)$ ．

查看试题解析
13. 9的算术平方根是， $\sqrt{0.16}$ = ， ﹣ $\sqrt[3]{\frac{8}{27}}$ = ．

查看试题解析
14. 如图，将长方形ABCD沿AE、DE折叠，使得点B＇、点C＇、点E在同一条直线上．若∠α=35°36′，则∠DEC的度数为．

查看试题解析
15. 已知关于x的一元一次方程 $x + 2 - \frac{1}{2019} x = m$ 的解是 $x = 71$ ，那么关于y的一元一次方程 $y + 3 - \frac{1}{2019} (y + 1) = m$ 的解是．

查看试题解析
16. 为了从n个外形相同的鸡蛋中找出唯一的一个双黄蛋，检查员将这些蛋按1－n的序号排成一列，第一次先从中取出序号为单数的蛋，发现其中没有双黄蛋；他将剩下的蛋在原来的位置上又按1、2、3，…编了序号（即原来的2号变为1号，原来的4号变为2号，…），又从中取出新序号为单数的蛋进行检查，仍没有发现双黄蛋；如此继续下去，检查到最后一个原始编号为8的蛋才是双黄蛋．那么n最大值是，如果最后找到的是原始编号为512的双黄蛋，则n的最大值是．

查看试题解析

三、解答题（共8小题，共66分）

17. 计算：

(1)、 $4 - (- 3) \times 2$

(2)、 ${(- \frac{3}{4})}^{2} \times （ - \frac{3}{2} ） \div \frac{3}{8}$

查看试题解析
18. 解方程：

(1)、 $3 x - (x - 1) = 5$

(2)、 $3 x - \frac{3 x - 1}{4} = 1$

查看试题解析
19. 一辆货车从百货大楼出发送货，向东行驶4千米到达小明家，继续向东行驶1.5千米到达小红家，然后向西行驶8.5千米到达小刚家，最后返回百货大楼．

(1)、以百货大楼为原点，向东为正方向，1个单位长度表示1千米，请你在数轴上标出小明、小红、小刚家的位置．（小明家用点A表示，小红家用点B表示，小刚家用点C表示）

(2)、小明家与小刚家相距多远？

查看试题解析
20. 先化简，再求值： $(2 x^{2} + x) - [4 x^{2} - (3 x^{2} - x)]$ ，其中 $x = - \frac{5}{3}$ ．

查看试题解析

21. 小李靠勤工俭学的收入支付上大学的费用，下面是小李某周的收支情况表，记收入为正，支出为负（单位：元）.

星期	一	二	三	四	五	六	七
收入	+65	+68	+50	+66	+50	+75	+74
支出	-60	-64	-63	-58	-60	-64	-65

(1)、到这个周末，小李有多少节余？

(2)、按以上的支出水平，估计小李一个月（按30天计算）至少有多少收入才能维持正常开支？

查看试题解析

22. 将大小不一的正方形纸片①、②、③、④放置在如图所示的长方形ABCD内（相同纸片之间不重叠），其中AB=a．

小明发现：通过边长的平移和转化，阴影部分⑤的周长与正方形①的边长有关.

(1)、根据小明的发现，用代数式表示阴影部分⑥的周长．

(2)、阴影部分⑥与阴影部分⑤的周长之差与正方形（填编号）的边长有关，请计算说明.

查看试题解析
23. 每年“双十一”购物活动，商家都会利用这个契机进行打折满减的促销活动．某商家平时的优惠措施是按所有商品标价打七折；“双十一”活动期间的优惠措施是：购买的所有商品先按标价总和打七五折，再享受折后每满200元减30元的优惠．
如标价为300元的商品，折后为225元，再减30元，即实付：300×0.75-30=195（元）．

(1)、该商店标价总和为1000元的商品，在“双十一“购买，最后实付只需多少元？

(2)、小明妈妈在这次活动中打算购买某件商品，打折满减后，应付金额是507元，求该商品的标价．

(3)、在（2）的条件下，若该商家出售的商品标价均为整数，小明通过计算后告诉妈妈：通过凑单的办法，只须再多支付元，就可以得到最大的优惠．

查看试题解析
24. 【阅读理解】射线OC是∠AOB内部的一条射线，若∠COA= $\frac{1}{2}$ ∠BOC，则我们称射线OC是射线OA的伴随线．

例如，如图1，∠AOB=60°，∠AOC=∠COD=∠BOD=20°，则∠AOC= $\frac{1}{2}$ ∠BOC，称射线OC是射线OA的伴随线；同时，由于∠BOD= $\frac{1}{2}$ ∠AOD，称射线OD是射线OB的伴随线．

(1)、【知识运用】如图2，∠AOB=120°，射线OM是射线OA的伴随线，则∠AOM=°，若∠AOB的度数是α，射线ON是射线OB的伴随线，射线OC是∠AOB的平分线，则∠NOC的度数是． (用含α的代数式表示)

(2)、【知识运用】如图3，如∠AOB=180°，射线OC与射线OA重合，并绕点O以每秒3°的速度逆时针旋转，射线OD与射线OB重合，并绕点O以每秒5°的速度顺时针旋转，当射线OD与射线OA重合时，运动停止．
①是否存在某个时刻t（秒），使得∠COD的度数是20°，若存在，求出t的值，若不存在，请说明理由．
②当t为多少秒时，射线OC、OD、OA中恰好有一条射线是其余两条射线的伴随线．

查看试题解析

x	-4	-3	-2	-1	0
2ax+5b	12	8	4	0	-4