浙江省湖州市吴兴区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-03-04 类型:期末考试
一、选择题(本题有10小题,每小题3分,共30分。每小题只有一个选项是正确的,不选、多选、错选均不给分)
-
1. 在平面直角坐标系中,点A(-2020,1)位于哪个象限?( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列长度的三条线段,能组成三角形的是( )A、3,4,8 B、5,6,10 C、5,5,11 D、5,6,113. 若三角形三个内角的度数比是2:3:4,则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定4. 不等式组 的解集在数轴上表示正确的是( )
A、 B、
B、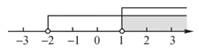 C、
C、 D、
D、 5. 如图,在Rt△ABC中,∠ABC=90º,BC=12,AB=5.分别以A,C为圆心,以大于线段AC长度的一半为半径作弧,两弧相交于点E,F,过点E,F作直线EF,交AC于点D,连结BD,则△ABD的周长为( )
5. 如图,在Rt△ABC中,∠ABC=90º,BC=12,AB=5.分别以A,C为圆心,以大于线段AC长度的一半为半径作弧,两弧相交于点E,F,过点E,F作直线EF,交AC于点D,连结BD,则△ABD的周长为( )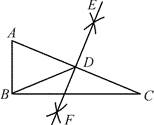 A、13 B、17 C、18 D、256. 关于x的一元一次不等式3x>6的解都能满足下列哪一个不等式的解( )
A、13 B、17 C、18 D、256. 关于x的一元一次不等式3x>6的解都能满足下列哪一个不等式的解( )
A、4x-9<x B、-3x+2<0 C、2x+4<0 D、7. 如图,直线 与直线 相交于点 ,则不等式 的解为( ) A、 B、 C、 D、8. 如图为小平与小聪微信对话记录,根据两人的对话记录,若下列有一种走法能从科技馆出发走到小平家,则可行的是( )
A、 B、 C、 D、8. 如图为小平与小聪微信对话记录,根据两人的对话记录,若下列有一种走法能从科技馆出发走到小平家,则可行的是( )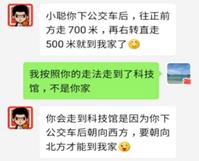 A、向北直走200米,再向东直走1200米 B、向北直走200米,再向西直走1200米 C、向北直走500米,再向东直走700米 D、向北直走700米,再向西直走500米9. 定义:△ABC中,一个内角的度数为 ,另一个内角的度数为 ,若满足 ,则称这个三角形为“准直角三角形”.如图,在Rt△ABC中,∠C=90°, AC=8,BC=6,D是BC上的一个动点,连接AD,若△ABD是“准直角三角形”,则CD的长是( )
A、向北直走200米,再向东直走1200米 B、向北直走200米,再向西直走1200米 C、向北直走500米,再向东直走700米 D、向北直走700米,再向西直走500米9. 定义:△ABC中,一个内角的度数为 ,另一个内角的度数为 ,若满足 ,则称这个三角形为“准直角三角形”.如图,在Rt△ABC中,∠C=90°, AC=8,BC=6,D是BC上的一个动点,连接AD,若△ABD是“准直角三角形”,则CD的长是( ) A、 B、 C、 D、10. 线段AB上有一动点C(不与A,B重合),分别以AC,BC为边向上作等边△ACM和等边△BCN,点D是MN的中点,连结AD,BD,在点C的运动过程中,有下列结论:①△ABD可能为直角三角形;②△ABD可能为等腰三角形;③△CMN可能为等边三角形;④若AB=6,则AD+BD的最小值为
A、 B、 C、 D、10. 线段AB上有一动点C(不与A,B重合),分别以AC,BC为边向上作等边△ACM和等边△BCN,点D是MN的中点,连结AD,BD,在点C的运动过程中,有下列结论:①△ABD可能为直角三角形;②△ABD可能为等腰三角形;③△CMN可能为等边三角形;④若AB=6,则AD+BD的最小值为 . 其中正确的是( )
. 其中正确的是( )  A、②③ B、①②③④ C、①③④ D、②③④
A、②③ B、①②③④ C、①③④ D、②③④二、填空题(本题有6小题,每小题4分,共24分)
-
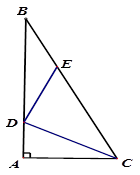
11. 已知一个正比例函数的图象经过点(-2,4),则这个正比例函数的表达式为 .12. 命题“全等三角形的对应角相等”的逆命题是命题(填“真”或“假”).13. 如图,直角△ABC中,∠A=90°,CD=DE=BE,当∠ACD=21°时,∠B=.
 14. 如图是一组密码的一部分,为了保密,许多情况下会采用不同的密码,请你运用所学知识找到破译的“密钥”.目前已破译出“守初心”的对应口令是“担使命”.根据你发现的“密钥”,破译出“找差距”的对应口令是 .
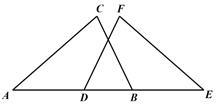
14. 如图是一组密码的一部分,为了保密,许多情况下会采用不同的密码,请你运用所学知识找到破译的“密钥”.目前已破译出“守初心”的对应口令是“担使命”.根据你发现的“密钥”,破译出“找差距”的对应口令是 . 15. 课本第78页阅读材料《从勾股定理到图形面积关系的拓展》中有如下问题:如图①分别以直角三角形的三条边为边,向形外分别作正三角形,则图中的 , , 满足的数量关系是. 现将△ABF向上翻折,如图②,已知 , , ,则△ABC的面积是.
15. 课本第78页阅读材料《从勾股定理到图形面积关系的拓展》中有如下问题:如图①分别以直角三角形的三条边为边,向形外分别作正三角形,则图中的 , , 满足的数量关系是. 现将△ABF向上翻折,如图②,已知 , , ,则△ABC的面积是. 16. 李刚和常明两人在数学活动课上进行折纸创编活动.
16. 李刚和常明两人在数学活动课上进行折纸创编活动.李刚拿起一张准备好的长方形纸片对常明说:“我现在折叠纸片(图①),使点D落在AB边的点F处,得折痕AE,再折叠,使点C落在AE边的点G处,此时折痕恰好经过点B,如果AD= ,那么AB长是多少?”常明说;“简单,我会. AB应该是”.
常明回答完,又对李刚说:“你看我的创编(图②),与你一样折叠,可是第二次折叠时,折痕不经过点B,而是经过了AB边上的M点,如果AD= ,测得EC=3BM,那么AB长是多少?”李刚思考了一会,有点为难,聪明的你,你能帮忙解答吗?AB=.

三、解答题(本题有8小题,共66分)
-
17. 解一元一次不等式组: .18. 在平面直角坐标系中,已知点M(m-1,2m+3)(1)、若点M在y轴上,求m的值.(2)、若点M在第一、三象限的角平分线上,求m的值.19. 已知:如图,点A,D,B,E在同一条直线上,∠ABC=∠EDF,AD=BE,BC=DF. 求证:AC=EF.
 20. 某电梯的额定限载量为1000千克.两人要用电梯把一批货物从底层搬到顶层,已知这两个人的体重分别为70千克和60千克,货物每箱重50千克,问他们每次最多只能搬运货物多少箱?21. 等腰三角形ABC的周长为16,腰AB长为 ,底边BC长为 ,求:(1)、y关于x的函数表达式;(2)、自变量x的取值范围;(3)、底边BC长为7时,腰长为多少?22. 等腰Rt△ABC,点D为斜边AB上的中点,点E在线段BD上,连结CD,CE,作AH⊥CE,垂足为H,交CD于点G,AH的延长线交BC于点F.
20. 某电梯的额定限载量为1000千克.两人要用电梯把一批货物从底层搬到顶层,已知这两个人的体重分别为70千克和60千克,货物每箱重50千克,问他们每次最多只能搬运货物多少箱?21. 等腰三角形ABC的周长为16,腰AB长为 ,底边BC长为 ,求:(1)、y关于x的函数表达式;(2)、自变量x的取值范围;(3)、底边BC长为7时,腰长为多少?22. 等腰Rt△ABC,点D为斜边AB上的中点,点E在线段BD上,连结CD,CE,作AH⊥CE,垂足为H,交CD于点G,AH的延长线交BC于点F.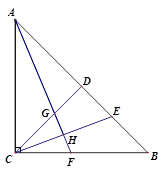 (1)、求证:△ADG≌△CDE.(2)、若点H恰好为CE的中点,求证:∠CGF=∠CFG.23. 某学校甲、乙两名同学去爱国主义教育基地参观,该基地与学校相距2400米.甲从学校步行去基地,出发5分钟后乙再出发,乙从学校骑自行车到基地. 乙骑行到一半时,发现有东西忘带,立即返回,拿好东西之后再从学校出发.在骑行过程中,乙的速度保持不变,最后甲、乙两人同时到达基地. 已知,乙骑行的总时间是甲步行时间的 .设甲步行的时间为 (分),图中线段OA表示甲离开学校的路程 (米)与 (分)的函数关系的图像.图中折线B—C—D和线段EA表示乙离开学校的路程 (米)与 (分)的函数关系的图像.
(1)、求证:△ADG≌△CDE.(2)、若点H恰好为CE的中点,求证:∠CGF=∠CFG.23. 某学校甲、乙两名同学去爱国主义教育基地参观,该基地与学校相距2400米.甲从学校步行去基地,出发5分钟后乙再出发,乙从学校骑自行车到基地. 乙骑行到一半时,发现有东西忘带,立即返回,拿好东西之后再从学校出发.在骑行过程中,乙的速度保持不变,最后甲、乙两人同时到达基地. 已知,乙骑行的总时间是甲步行时间的 .设甲步行的时间为 (分),图中线段OA表示甲离开学校的路程 (米)与 (分)的函数关系的图像.图中折线B—C—D和线段EA表示乙离开学校的路程 (米)与 (分)的函数关系的图像.
根据图中所给的信息,解答下列问题:
(1)、甲步行的速度和乙骑行的速度;(2)、甲出发多少时间后,甲、乙两人第二次相遇?(3)、若 (米)表示甲、乙两人之间的距离,当 时,求 (米)关于 (分)的函数关系式.24. 已知,一次函数 的图像与 轴、 轴分别交于点A、点B,与直线 相交于点C.过点B作 轴的平行线l.点P是直线l上的一个动点.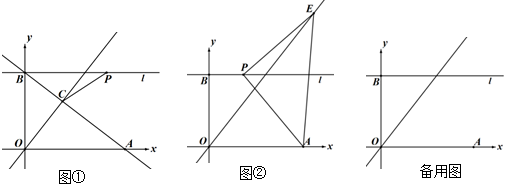 (1)、求点A,点B的坐标.(2)、若 ,求点P的坐标.(3)、若点E是直线 上的一个动点,当△APE是以AP为直角边的等腰直角三角形时,求点E的坐标.
(1)、求点A,点B的坐标.(2)、若 ,求点P的坐标.(3)、若点E是直线 上的一个动点,当△APE是以AP为直角边的等腰直角三角形时,求点E的坐标.