备考2020年中考数学二轮复习拔高训练卷专题1 数与式

试卷更新日期：2020-03-03 类型：二轮复习

进入出卷网下载

一、单选题

1. 下列计算正确的是（　　）

A、2³=6 B、-4²=-16 C、-8-8=0 D、-5-2=-3

查看试题解析
2. 已知 $a ， b$ 两数在数轴上的位置如图所示，则化简代数式 $| a + b | - | a - 1 | + | b + 2 |$ 的结果是（）

A、1 B、 $2 a - 3$ C、2b+3 D、－1

查看试题解析
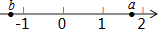3. 设边长为3的正方形的对角线长为a，下列关于a的四种说法：① a是无理数；② a可以用数轴上的一个点来表示；③ 3<a<4；④ a是18的算术平方根。其中，所有正确说法的序号是( )

A、①④ B、②③ C、①②④ D、①③④

查看试题解析
4. 把代数式(a－1) $\sqrt{\frac{1}{1 - a}}$ 的a－1移到根号内，那么这个代数式等于（）

A、－ $\sqrt{1 - a}$ B、 $\sqrt{a - 1}$ C、 $\sqrt{1 - a}$ D、－ $\sqrt{a - 1}$

查看试题解析
5. 如图，从左上角标注2的圆圈开始，顺时针方向按an+b的规律，（n表示前一个圆圈中的数字，a，b是常数）转换后得到下一个圆圈中的数，则标注“？”的圆圈中的数应是（）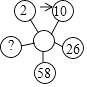

A、119 B、120 C、121 D、122

查看试题解析
6.
如图，弹性小球从P（2，0）出发，沿所示方向运动，每当小球碰到正方形OABC的边时反弹，反弹时反射角等于入射角，当小球第一次碰到正方形的边时的点为P₁ ，第二次碰到正方形的边时的点为P₂…第n次碰到正方形的边时的点为P_n ，则P₂₀₁₅的坐标是（　　）

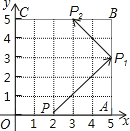A、（5，3） B、（3，5） C、（0，2） D、（2，0）

查看试题解析
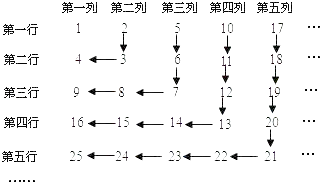
7.
若正整数按如图所示的规律排列，则第8行第5列的数字是（）

A、64 B、56 C、58 D、60

查看试题解析
8. 已知a＋ $\frac{1}{a}$ ＝ $\sqrt{10}$ ，则a－ $\frac{1}{a}$ 的值为（）

A、±2 $\sqrt{2}$ B、8 C、 $\sqrt{6}$ D、± $\sqrt{6}$

查看试题解析
9.
如图，在平面直角坐标系中，点P坐标为（-2，3），以点O为圆心，以OP的长为半径画弧，交x轴的负半轴于点A，则点A的横坐标介于（）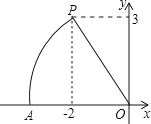

A、－4和－3之间 B、3和4之间 C、－5和－4之间 D、4和5之间

查看试题解析
10. 对于实数a，b，定义运算“*”：a*b=a²-ab（a≤b）； a*b=b²-ab（a>b），关于x的方程（2x-1)*(x-1)=m 恰好有三个不相等的实数根，则m的取值范围是（）

A、m> $\frac{1}{4}$ B、 $0 < m < \frac{1}{4}$ C、 $- \frac{1}{4} < m < 0$ D、 $m < - \frac{1}{4}$

查看试题解析

二、填空题

11. 计算1+4+9+16+25+…的前29项的和是．

查看试题解析
12. 若a是一个完全平方数，则比a大的最小完全平方数是。

查看试题解析
13. 在有理数范围内分解因式：（x+1）（x+2）（2x+3）（x+6）-20x⁴= ．

查看试题解析
14. 我们把分子为1的分数叫做理想分数，如 $\frac{1}{2}$ ， $\frac{1}{3}$ ， $\frac{1}{4}$ ，…，任何一个理想分数都可以写成两个不同理想分数的和，如 $\frac{1}{2} = \frac{1}{3} + \frac{1}{6}$ ， $\frac{1}{3} = \frac{1}{4} + \frac{1}{12}$ ， $\frac{1}{4} = \frac{1}{5} + \frac{1}{20}$ ，…根据对上述式子的观察，请你思考：如果理想分数 $\frac{1}{n} = \frac{1}{a} + \frac{1}{b}$ (n是不小于2的整数，且a＜b)，那么b－a＝． (用含n的式子表示)

查看试题解析
15. 如图，在平面直角坐标系中，将 $△ A B O$ 绕点 $B$ 顺时针旋转到 $△ A_{1} B_{1} O_{2}$ 的位置，使点 $O_{1}$ 的对应点 $O_{2}$ 落在直线 $y = \frac{\sqrt{3}}{3} x$ 上……，依次进行下去，若点 $A$ 的坐标是（0，1），点 $B$ 的坐标是 $(\sqrt{3} ， 1)$ ，则点 $A_{8}$ 的横坐标是.

查看试题解析

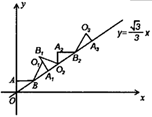
三、解答题

16. 已知2a﹣1的平方根是±3，3a+b+9的立方根是3，求2（a+b）的平方根．

查看试题解析
17. 若a＞0，b＜0，且|x-a|+|x-b|=a-b，求x的取值范围．

查看试题解析
18. 设 $3 x^{2} + a x + b$ 与 $2 x^{2} - 4 x + 5$ 的乘积不含三次项与一次项，求a、b的值．

查看试题解析
19. 若 $\frac{x}{3} = \frac{y}{4} = \frac{z}{5}$ ，且4x-5y+2z=10，求2x-5y+z的值．

查看试题解析
20. 先化简： $\frac{x}{x + 3}$ ÷ $\frac{x^{2} + x}{x^{2} + 6 x + 9}$ + $\frac{3 x - 3}{x^{2} - 1}$ ，再求当x+1与x+6互为相反数时代数式的值．

查看试题解析
21. 某快递公司有甲、乙、丙三个机器人分配快件，甲单独完成需要x小时，乙单独完成需要y小时，丙单独完成需要z小时．

(1)、求甲单独完成的时间是乙丙合作完成时间的几倍？

(2)、若甲单独完成的时间是乙丙合作完成时间的a倍，乙单独完成的时间是甲丙合作完成时间的b倍，丙单独完成的时间是甲乙合作完成时间的c倍，求 $\frac{1}{a + 1} + \frac{1}{b + 1} + \frac{1}{c + 1}$ 的值．

查看试题解析
22. 某商场在世界杯足球比赛期间举行促销活动，并设计了两种方案：一种是以商品价格的九五折优惠的方式进行销售；一种是采用有奖销售的方式，具体措施是：①有奖销售自2009年6月9日起，发行奖券10000张，发完为止；②顾客累计购物满400元，赠送奖券一张（假设每位顾客购物每次都恰好凑足400元）；③世界杯后，顾客持奖券参加抽奖；④奖项是：特等奖2名，各奖3000元奖品；一等奖10名，各奖1000元奖品；二等奖20名，各奖300元奖品；三等奖100名，各奖100元奖品；四等奖200名，各奖50元奖品；纪念奖5000名，各奖10元奖品，试就商场的收益而言，对两种促销方法进行评价，选用哪一种更为合算？

查看试题解析

备考2020年中考数学二轮复习拔高训练卷 专题1 数与式

一、单选题

二、填空题

三、解答题

备考2020年中考数学二轮复习拔高训练卷专题1 数与式