2016-2017学年湖北省宜昌市七校教学协作体高二下学期期末数学试卷（理科）

试卷更新日期：2017-08-17 类型：期末考试

进入出卷网下载

一、选择题

1. 如果复数z= $\frac{2}{- 1 + i}$ ，则（）

A、|z|=2 B、z的实部为1 C、z的虚部为﹣1 D、z的共轭复数为1+i

查看试题解析
2. 某地区高中分三类，A类学校共有学生2000人，B类学校共有学生3000人，C类学校共有学生4000人，若采取分层抽样的方法抽取900人，则A类学校中的学生甲被抽到的概率为（）

A、 $\frac{1}{10}$ B、 $\frac{9}{20}$ C、 $\frac{1}{2000}$ D、 $\frac{1}{2}$

查看试题解析
3. 已知命题p：若x＜﹣3，则x²﹣2x﹣8＞0，则下列叙述正确的是（）

A、命题p的逆命题是：若x²﹣2x﹣8≤0，则x＜﹣3 B、命题p的否命题是：若x≥﹣3，则x²﹣2x﹣8＞0 C、命题p的否命题是：若x＜﹣3，则x²﹣2x﹣8≤0 D、命题p的逆否命题是真命题

查看试题解析
4. 从数字0，1，2，3，4，5中任选3个数字，可组成没有重复数字的三位数共有（）

A、60 B、90 C、100 D、120

查看试题解析
5. 已知命题p：∃x₀∈R，x₀²﹣2x₀+3≤0的否定是∀x∈R，x²﹣2x+3＞0，命题q：双曲线 $\frac{x^{2}}{4}$ ﹣y²=1的离心率为2，则下列命题中为真命题的是（）

A、p∨q B、￢p∧q C、￢p∨q D、p∧q

查看试题解析
6. 一名法官在审理一起珍宝盗窃案时，四名嫌疑人甲、乙、丙、丁的供词如下，甲说：“罪犯在乙、丙、丁三人之中”：乙说：“我没有作案，是丙偷的”：丙说：“甲、乙两人中有一人是小偷”：丁说：“乙说的是事实”．经过调查核实，四人中有两人说的是真话，另外两人说的是假话，且这四人中只有一人是罪犯，由此可判断罪犯是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 某学校为了调查喜欢语文学科与性别的关系，随机调查了一些学生情况，具体数据如表：
调查统计
不喜欢语文
喜欢语文
男
13
10
女
7
20
为了判断喜欢语文学科是否与性别有关系，根据表中的数据，得到K²的观测值k= $\frac{50 \times (13 \times 20 - 10 \times 7) 2}{23 \times 27 \times 20 \times 30}$ ≈4.844，因为k≥3.841，根据下表中的参考数据：
P（K²≥k₀）
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k₀
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
判定喜欢语文学科与性别有关系，那么这种判断出错的可能性为（）

A、95% B、50% C、25% D、5%

查看试题解析
8. 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．下图是源于其思想的一个程序框图，若输入的a，b分别为5，2，则输出的n=（）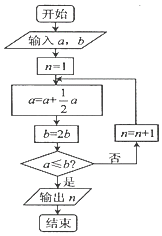

A、2 B、3 C、4 D、5

查看试题解析
9. 如图，长方体ABCD﹣A₁B₁C₁D₁中，AA₁=AB=2，AD=1点E，F，G分别是DD₁ ， AB，CC₁的中点，则异面直线A₁E与GF所成的角是（）

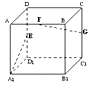A、90° B、60° C、45° D、30°

查看试题解析
10. 在（ $\frac{x}{2} - \frac{1}{\sqrt[3]{x}}$ ）ⁿ的展开式中，只有第5项的二项式系数最大，则展开式的常数项为（）

A、﹣7 B、7 C、﹣28 D、28

查看试题解析
11. 设抛物线y²=4x的准线与x轴交于点Q，若过点Q的直线l与抛物线有公共点，则直线l的斜率的取值范围是（）

A、[﹣ $\frac{1}{2}$ ， $\frac{1}{2}$ ] B、[﹣2，2] C、[﹣1，1] D、[﹣4，4]

查看试题解析
12. 关于x的方程x³﹣ax+2=0有三个不同实数解，则实数a的取值范围是（）

A、（2，+∞） B、（3，+∞） C、（0，3 ） D、（﹣∞，3）

查看试题解析

二、填空题

13. 已知x和y之间的一组数据，若x、y具有线性相关关系，且回归方程为 $\hat{y}$ =x+a，则a的值为．
x
0
1
2
3
y
1
3
5
7

查看试题解析
14. 函数f（x）=x³﹣3x²+1在x₀处取得极小值，则x₀= ．

查看试题解析
15. 如图，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为．

查看试题解析
16. 已知P是直线3x+4y+8=0上的动点，PA，PB是圆x²+y²﹣2x﹣2y+1=0的两条切线，A，B是切点，C是圆心，那么四边形PACB面积的最小值为．

查看试题解析

三、解答题

17. 已知数列 $\frac{1}{1 \times 3} ， \frac{1}{3 \times 5} ， \frac{1}{5 \times 7} ， \dots ， \frac{1}{(2 n - 1) (2 n + 1)}$ ，…，S_n是其前n项和，计算S₁、S₂、S₃ ，由此推测计算S_n的公式，并给出证明．

查看试题解析
18. 为调查大学生这个微信用户群体中每人拥有微信群的数量，现从武汉市大学生中随机抽取100位同学进行了抽样调查，结果如下：
微信群数量
频数
频率
0至5个
0
0
6至10个
30
0.3
11至15个
30
0.3
16至20个
a
c
20个以上
5
b
合计
100
1
（Ⅰ）求a，b，c的值；
（Ⅱ）以这100个人的样本数据估计武汉市的总体数据且以频率估计概率，若从全市大学生（数量很大）中随机抽取3人，记X表示抽到的是微信群个数超过15个的人数，求X的分布列和数学期望．

查看试题解析
19. 如图，在三棱柱ABC﹣A₁B₁C₁中，侧面AA₁C₁C底面ABC，AA₁=A₁C=AC=AB=BC=2，且点O为AC中点．
（Ⅰ）证明：A₁O⊥平面ABC；
（Ⅱ）求二面角A₁﹣AB﹣C的余弦值．

查看试题解析
20. 2016年年初为迎接习总书记并向其报告工作，省有关部门从南昌大学校企业的LED产品中抽取1000件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图：
（Ⅰ）求这1000件产品质量指标值的样本平均数 $\bar{x}$ 和样本方差s²（同一组数据用该区间的中点值作代表）；
（Ⅱ）由频率分布直方图可以认为，这种产品的质量指标值Z服从正态分布N（μ，δ²），其中μ近似为样本平均数 $\bar{x}$ ，δ²近似为样本方差s² ．
（i）利用该正态分布，求P（175.6＜Z＜224.4）；
（ii）某用户从该企业购买了100件这种产品，
记X表示这100件产品中质量指标值为于区间 $({175.6}_{}^{} ，_{}^{} 224.4)$ 的产品件数，利用（i）的结果，求EX．
附： $\sqrt{150}$ ≈12.2．若Z～N（μ，δ²），则P（μ﹣δ＜Z＜μ+δ）=0.6826，P（μ﹣2δ＜Z＜μ+2δ）=0.9544．

查看试题解析
21. 已知椭圆E的右焦点与抛物线y²=4x的焦点重合，点M $(1 ， \frac{3}{2})$ 在椭圆E上．
（Ⅰ）求椭圆E的标准方程；
（Ⅱ）设P（﹣4，0），直线y=kx+1与椭圆E交于A，B两点，若直线PA，PB关于x轴对称，求k的值．

查看试题解析
22. 已知函数f（x）=alnx﹣x²+1．
（Ⅰ）若曲线y=f（x）在x=1处的切线方程为4x﹣y+b=0，求实数a和b的值；
（Ⅱ）讨论函数f（x）的单调性；
（Ⅲ）若a＜0，且对任意x₁ ， x₂∈（0，+∞），x₁≠x₂ ，都有|f（x₁）﹣f（x₂）|＞|x₁﹣x₂|，求a的取值范围．

查看试题解析

P（K²≥k₀）	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k₀	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

微信群数量	频数	频率
0至5个	0	0
6至10个	30	0.3
11至15个	30	0.3
16至20个	a	c
20个以上	5	b
合计	100	1

调查统计	不喜欢语文	喜欢语文
男	13	10
女	7	20