2015年高考理数真题试卷（湖北卷）

试卷更新日期：2016-04-12 类型：高考真卷

进入出卷网下载

一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的

1. $i$ 为虚数单位， $i^{607}$ 的共轭复数为（）

A、 $i$ B、- $i$ C、1 D、-1

查看试题解析
2. 我国古代数学名著《九章算术》有“米谷粒分”题：粮仓开仓收粮，有人送来米1534石，验得米内夹谷，抽样取米一把，数得254内夹谷28粒，则这批米内夹谷约为（）

A、134石 B、169石 C、338石 D、1365石

查看试题解析
3. 已知 ${(1 + x)}^{π}$ 的展开式中第4项与第8项的二项式系数相等，则奇数项的二项式系数和为（）

A、 $2^{12}$ B、 $2^{11}$ C、 $2^{10}$ D、 $2^{9}$

查看试题解析
4. 设 $X - N (μ_{1} ， σ_{1}^{2}) ， Y - N (μ_{2} ， σ_{2}^{2})$ ，这两个正态分布密度曲线如图所示．下列结论中正确的是（）

A、 $P (Y \geq μ_{2}) \geq P (Y \geq μ_{1})$ B、 $P (X \leq σ_{2}) \leq P (X \leq σ_{1})$ C、对任意正数 $t$ ， $p (X \leq t) \geq p (Y \leq t)$ D、对任意正数 $t$ ， $P (X \geq t) \geq P (Y \geq t)$

查看试题解析
5. 设 $a_{1} ， a_{2 ，} \cdot \cdot \cdot ， a_{π} \in R ， n \geq 3$ . 若p： $a_{1} ， a_{2} ， \dots ， a_{π}$ 成等比数列；
q： $(a_{1}^{2} + a_{2}^{2} + \dots + a_{π}^{2}) (a_{2}^{2} + a_{3}^{2} + \dots + a_{π}^{2}) = {(a_{1} a_{2} + a_{2} a_{3} + \dots + a_{π - 1} a_{π})}^{2}$ ，则（）

A、p是q的充分条件，但不是q的必要条件 B、p是q的必要条件，但不是q的充分条件 C、p是q的充分必要条件 D、p既不是q的充分条件，也不是q的必要条件

查看试题解析
6. .已知符号函数 $s g n x = \{\begin{matrix} 1 ， x > 0 \\ 0 ， x = 0 \\ - 1 ， x < 0 \end{matrix}$ $f (x)$ 是R上的增函数， $g (x) = f (x) - f (a x) (a > 1)$ ，则（）

A、 $s g n [g (x)] = s g n x$ B、 $s g n [g (x)] = - s g n x$ C、 $s g n [g (x)] = s g n [f (x)]$ D、 $s g n [g (x)] = - s g n [f (x)]$

查看试题解析
7. 在区间 $[0 ， 1]$ 上随机取两个数 $x ， y$ ，记 $p_{1}$ 为事件“ $x + y \geq \frac{1}{2}$ ”的概率， $p_{2}$ 为事件“ $|x - y| \leq \frac{1}{2}$ ”的概率， $p_{3}$ 为事件“ $x y \leq \frac{1}{2}$ ”的概率，则（）

A、 $p_{1} < p_{2} < p_{3}$ B、 $p_{2} < p_{3} < p_{1}$ C、 $p_{3 <} p_{1} < p_{2}$ D、 $p_{3 <} p_{2} < p_{1}$

查看试题解析
8. 将离心率为 $e_{1}$ 的双曲线 $c_{1}$ 的实半轴长 $a$ 和虚半轴长 $b (a \neq b)$ 同时增加 $m (m > 0)$ 个单位长度，得到离心率为 $e_{2}$ 的双曲线 $c_{2}$ ，则（）

A、对任意的 $a ， b$ ， $e_{1} > e_{2}$ B、当 $a > b$ 时， $e_{1} > e_{2}$ ；当 $a < b$ 时， $e_{1} < e_{2}$ C、对任意的 $a ， b$ ， $e_{1} < e_{2}$ D、当 $a > b$ 时， $e_{1} < e_{2}$ ；当 $a < b$ 时， $e_{1} > e_{2}$

查看试题解析
9. 已知集合 $A = {(x ， y) | x^{2} + y^{2} \leq 1 ， x ， y \in Z}$ ， $B = {(x ， y) | |x| \leq 2 ， |y| \leq 2 ， x ， y \in Z}$ ，定义集合 $A \oplus B = {(x_{1} + x_{2} ， y_{1} + y_{2}) | (x_{1} ， y_{1}) \in A ， (x_{2} ， y_{2}) \in B}$ ，则 $A \oplus B$ 中元素的个数为（）

A、77 B、49 C、45 D、30

查看试题解析
10. 设整数. 若存在实数 $t$ ，使得 $[t] = 1$ ， $[t^{2}] = 2$ ， …， $[t^{n}] = n$
同时成立，则正整数n的最大值是（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题：本大题共5小题，每小题5分，共25分

11. 已知向量AB $\vec{O A} ⊥ \vec{A B}$ ， $|\vec{O A}| = 3$ ，则 $\vec{O A} \cdot \vec{O B} =$ .

查看试题解析
12. 函数 $f (x) = 4 \cos^{2} \frac{x}{2} \cos (\frac{π}{2} - x) - 2 \sin x - |\ln (x + 1)|$ 的零点个数为．

查看试题解析
13. 如图，一辆汽车在一条水平的公路上向正西行驶，到A处时测得公路北侧一山顶D在西偏北 $30^{\circ}$ 的
方向上，行驶600m后到达B处，测得此山顶在西偏北 $75^{\circ}$ 的方向上，仰角为 $30^{\circ}$ ，则此山的高度 $C D =$ m.

查看试题解析
14. 如图，PA是圆的切线，A为切点，PBC是圆的割线，且 $B C = 3 P B$ ，则 $\frac{A B}{A C} =$ .

查看试题解析
15. （选修4-4：坐标系与参数方程）

在直角坐标系xOy中，以O为极点， $x$ 轴的正半轴为极轴建立极坐标系. 已知直线 $l$ 的极坐标方程为 $p (\sin θ - 3 \cos θ) = 0$ ，曲线C的参数方程为 $\{\begin{matrix} x = t - \frac{1}{t} ， \\ y = t + \frac{1}{t} \end{matrix}$ ( t为参数) ， $l$ 与C相交于 $A ， B$ 两点，则 $|A B| =$ .

查看试题解析

三、解答题

16. 某同学用“五点法”画函数 $f (x) = A \sin (ω x + φ) (ω > 0 ， |φ| < \frac{π}{2})$ 在某一个周期内的图象时，列表并填入了部分数据，如下表：
$ω x + φ$
0
$\frac{π}{2}$
$π$
$\frac{3 π}{2}$
$2 π$
x

$\frac{π}{3}$

$\frac{5 π}{6}$

$A \sin (ω x + φ)$
0
5

-5
0
（Ⅰ）请将上表数据补充完整，填写在答题卡上相应位置，并直接写出函数 $f (x)$ 的解析式；
（Ⅱ）将 $y = f (x)$ 图象上所有点向左平行移动 $θ (θ > 0)$ 个单位长度，得到 $y = g (x)$ 的图象. 若 $y = g (x)$ 图象的一个对称中心为 $(\frac{5 π}{12} ， 0)$ ，求 $θ$ 的最小值.

查看试题解析
17. 设等差数列 $\{a_{n}\}$ 的公差为d，前n项和为 $s_{n}$ ，等比数列 $\{b_{n}\}$ 的公比为q．已知 $b_{1} = a_{1}$ ， $b_{2} = 2$ ， $q = d$ ， $s_{10} = 100$ ．

(1)、求数列 $\{a_{n}\}$ ， $\{b_{n}\}$ 的通项公式；

(2)、当 $d > 1$ 时，记 $c_{n} = \frac{a_{n}}{b_{n}}$ ，求数列 $\{c_{n}\}$ 的前 $n$ 项和 $T_{n}$ ．

查看试题解析
18. 《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．
如图，在阳马P-ABCD中，侧棱 $P D ⊥$ 底面 $A B C D$ ，且 $P D = C D$ ，过棱 $P C$ 的中点 $E$ ，作 $E F ⊥ P B$ 交 $P B$ 于点 $F$ ，连接 $D E ， D F ， B D ， B E$

(1)、证明： $P B ⊥$ 平面 $D E F$ ．试判断四面体 $D B E F$ 是否为鳖臑，若是，写出其每个面的直角（只需写
出结论）；若不是，说明理由；

(2)、若面 $D E F$ 与面 $A B C D$ 所成二面角的大小为 $\frac{π}{3}$ ，求 $\frac{D C}{B C}$ 的值．

查看试题解析
19. 某厂用鲜牛奶在某台设备上生产 $A ， B$ 两种奶制品．生产1吨A产品需鲜牛奶2吨，使用设备1小时，获利1000元；生产1吨B产品需鲜牛奶1.5吨，使用设备1.5小时，获利1200元．要求每天B产品的产量不超过A产品产量的2倍，设备每天生产 $A ， B$ 两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W（单位：吨）是一个随机变量，其分布列为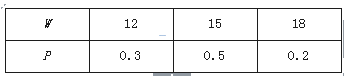
（Ⅰ）求Z的分布列和均值；该厂每天根据获取的鲜牛奶数量安排生产，使其获利最大，因此每天的最大获利Z（单位：元）是一个随机变量．
（Ⅱ）若每天可获取的鲜牛奶数量相互独立，求3天中至少有1天的最大获利超过10000元的概率．

查看试题解析
20. 一种作图工具如图1所示．O是滑槽AB的中点，短杆ON可绕O转动，长杆MN通过N处铰链与ON连接，MN上的栓子D可沿滑槽AB滑动，且 $D N = O N = 1$ ， $M N = 3$ ．当栓子D在滑槽AB内作往复运动时，带动N绕O转动一周（D不动时，N也不动），M处的笔尖画出的曲线记为C．以O为原点，AB所在的直线为 $x$ 轴建立如图2所示的平面直角坐标系。

(1)、求曲线C的方程；

(2)、设动直线 $l$ 与两定直线 $l ： x - 2 y = 0$ 和 $l_{2} ： x + 2 y = 0$ 分别交于 $p ， Q$ 两点．若直线 $l$ 总与曲线C有且只有一个公共点，试探究： $△ O Q P$ 的面积是否存在最小值？若存在，求出该最小值；若不存在，说明理由．

查看试题解析
21. 已知数列 $\{a_{n}\}$ 的各项均为正数， $b_{n} = n {(1 + \frac{1}{n})}^{n} a_{n} (n \in N_{+})$ ， $e$ 为自然对数的底数．

(1)、求函数 $f (x) = 1 + x - e^{x}$ 的单调区间，并比较 ${(1 + \frac{1}{n})}^{n}$ 与 $e$ 的大小；

(2)、计算 $\frac{b_{1}}{a}$ ， $\frac{b_{1} b_{2}}{a_{1} a_{2}}$ ， $\frac{b_{1} b_{2} b_{3}}{a_{1} a_{2} a_{3}}$ ，由此推测计算 $\frac{b_{1} b_{2} \dots b_{n}}{a_{1} a_{2} \dots a_{n}}$ 的公式，并给出证明；

(3)、令 $c_{n} = {(a_{1} a_{2} \dots a_{n})}^{\frac{1}{n}}$ ，数列 $\{a_{n}\}$ ， $\{c_{n}\}$ 的前 $n$ 项和分别记为 $s_{n}$ ， $T_{n}$ ，证明： $T_{n} < e S_{n}$ .

查看试题解析

$ω x + φ$	0	$\frac{π}{2}$	$π$	$\frac{3 π}{2}$	$2 π$
x		$\frac{π}{3}$		$\frac{5 π}{6}$
$A \sin (ω x + φ)$	0	5		-5	0