2015年高考理数真题试卷(安徽卷)
试卷更新日期:2016-04-12 类型:高考真卷
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的
-
1. 设i是虚数单位,则复数在复平面内所对应的点位于()A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列函数中,既是偶函数又存在零点的是A、y=COSx B、y=SINx C、y=lnx D、y=+13. 设p:1x1,q:1,则p是q成立的A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件4. 下列双曲线中,焦点在y轴上且渐近线方程为y=2x的是()A、 B、 C、 D、5. 已知m,n是两条不同直线, , 是两个不同平面,则下列命题正确的是A、若 , 垂直于同一平面,则与平行 B、若m,n平行于同一平面,则m与n平行 C、若 , 不平行,则在内不存在与平行的直线 D、若m,n不平行,则m与n不可能垂直于同一平面6. 若样本数据x1,x2,...,x10的标准差为8,则数据2x1-1,2x2-1,...,2x10-1的标准差为A、8 B、15 C、16 D、327. 一个四面体的三视图如图所示,则该四面体的表面积是
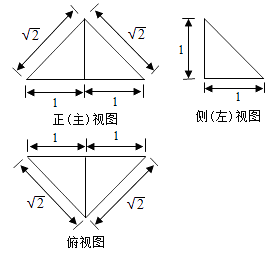 A、 B、 C、 D、8. 是边长为2的等边三角形,已知向量 , 满足=2 , =2+ , 则下列结论正确的是A、=1 B、 C、.=1 D、9. 函数f(x)=的图像如图所示,则下列结论成立的是
A、 B、 C、 D、8. 是边长为2的等边三角形,已知向量 , 满足=2 , =2+ , 则下列结论正确的是A、=1 B、 C、.=1 D、9. 函数f(x)=的图像如图所示,则下列结论成立的是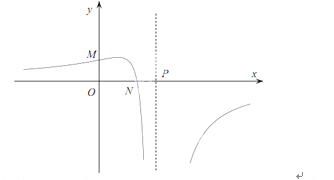 A、a0,b0,c0 B、a0,b0,c0 C、a0,b0,c0 D、a0,b0,c010. 已知函数f(x)=Asin(+)(A, , 均为正的常数)的最小正周期为 , 当x=时,函数f(x)取得最小值,则下列结论正确的是A、f(2)f(-2)f(0) B、f(0)f(2)f(-2) C、f(-2)f(0)f(2) D、f(2)f(0)f(-2)
A、a0,b0,c0 B、a0,b0,c0 C、a0,b0,c0 D、a0,b0,c010. 已知函数f(x)=Asin(+)(A, , 均为正的常数)的最小正周期为 , 当x=时,函数f(x)取得最小值,则下列结论正确的是A、f(2)f(-2)f(0) B、f(0)f(2)f(-2) C、f(-2)f(0)f(2) D、f(2)f(0)f(-2)二、填空题:本大题5小题,每小题5分,共25分,把答案填在答题卡相应的位置
-
11. (x3+)的展开式中x5的系数是12. 在极坐标中,圆P=8sin上的点到直线=(pR)距离最大值是 。13. 执行如图所示的程序框图(算法流程图),输出的n 。
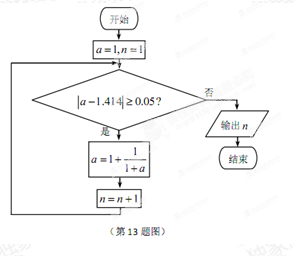 14. 已知数列 是递增的等比数列,a1+a4=9,a2a3=8,则数列 的前n项和等于 。15. 设x3+ax+b=0,其中a,b均为实数,下列条件中,使得该三次方程中仅有一个实根的是 ,(写出所有正确条件的编号)
14. 已知数列 是递增的等比数列,a1+a4=9,a2a3=8,则数列 的前n项和等于 。15. 设x3+ax+b=0,其中a,b均为实数,下列条件中,使得该三次方程中仅有一个实根的是 ,(写出所有正确条件的编号)1、a=-3,b=-3;2.a=-3,b=2;3、a=-3,b2;4、a=0,b=2;5、a=1,b=2
三、解答题:本大题6小题,共75分,解答时应写出文字说明、证明过程或演算步骤,解答写在答题卡上的制定区域内
-
16. 在中,A= , AB=6,AC=3 , 点D在BC边上,AD=BD,求AD的长17. 已知2件次品和3件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所 需要的检测费用(单位:元),求X的分布列和均值(数学期望).
四、综合题
-
18. 设 , Xn是曲线y=X2n+2+1在点(1,2)处的切线与x轴焦点的横坐标(1)、求数列{xn}的通项公式;(2)、记Tn=.... , 证明Tn19. 如图所示,在多面体A1B1D1-DCBA中,四边形AA1B1B,ADD1A1 , ABCD均为正方形,E为B1D1的中点 ,过A1 , D,E的平面交CD 1于F。
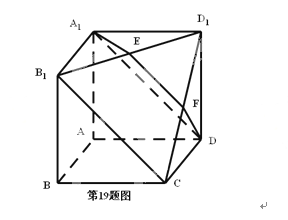 (1)、证明:EF∥B1C(2)、求二面角E-A1D-B1的余弦。20. 设椭圆E的方程为+=1(ab0),点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足=2 , 直线OM的斜率为。(1)、求E的离心率e。(2)、设点C的坐标为(0,-b),N为线段AC的中点,点N关于直线AB的对称点的纵坐标为 , 求E的方程21. 设函数f(x)=x2-ax+b,问:(1)讨论函数f(sinx)在( , )内的单调性并判断有无极值,有极值时求出极值;(2)记f0(x)= - x + ,求函数| f ( sin x ) - ( sin x )| 在[ . ]上的最大值D,(3)在(2)中,取a0=b0=0,求z= b - 满足D ≤ 1时的最大值
(1)、证明:EF∥B1C(2)、求二面角E-A1D-B1的余弦。20. 设椭圆E的方程为+=1(ab0),点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足=2 , 直线OM的斜率为。(1)、求E的离心率e。(2)、设点C的坐标为(0,-b),N为线段AC的中点,点N关于直线AB的对称点的纵坐标为 , 求E的方程21. 设函数f(x)=x2-ax+b,问:(1)讨论函数f(sinx)在( , )内的单调性并判断有无极值,有极值时求出极值;(2)记f0(x)= - x + ,求函数| f ( sin x ) - ( sin x )| 在[ . ]上的最大值D,(3)在(2)中,取a0=b0=0,求z= b - 满足D ≤ 1时的最大值
(1)、讨论函数f(sinx)在( , )内的单调性并判断有无极值,有极值时求出极值;
(2)、记f0(x)= , 求函数在上的最大值D,
(3)、在(2)中,取a0=b0=0,求z=满足D1时的最大值