福建省龙岩市2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-02-27 类型:期末考试
一、单选题
-
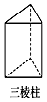
1. 如图,在下面的四个几何体中,从它们各自的正面和左面看,不相同的是( )A、
 B、
B、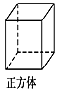 C、
C、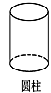 D、
D、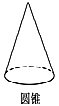 2. 中国华为麒麟985处理器是采用7纳米制程工艺的手机芯片,在指甲盖大小的尺寸上塞进了120亿个晶体管,是世界上最先进的具有人工智能的手机处理器,将120亿个用科学记数法表示为( )A、 个 B、 个 C、 个 D、 个3. 下列计算正确是( )A、3a+2a=5a2 B、3a-a=3 C、2a3+3a2=5a5 D、-a2b+2a2b=a2b4. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“点”字所在面相对面上的汉字是( )
2. 中国华为麒麟985处理器是采用7纳米制程工艺的手机芯片,在指甲盖大小的尺寸上塞进了120亿个晶体管,是世界上最先进的具有人工智能的手机处理器,将120亿个用科学记数法表示为( )A、 个 B、 个 C、 个 D、 个3. 下列计算正确是( )A、3a+2a=5a2 B、3a-a=3 C、2a3+3a2=5a5 D、-a2b+2a2b=a2b4. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“点”字所在面相对面上的汉字是( )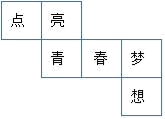 A、青 B、春 C、梦 D、想5. 下列判断中正确是 ( )A、 与 不是同类项 B、 不是整式 C、单项式 的系数是 -1 D、 是二次三项式6. 已知a-b=-3,c+d=2,则(b+c)-(a-d)的值为( )
A、青 B、春 C、梦 D、想5. 下列判断中正确是 ( )A、 与 不是同类项 B、 不是整式 C、单项式 的系数是 -1 D、 是二次三项式6. 已知a-b=-3,c+d=2,则(b+c)-(a-d)的值为( )
A、1 B、5 C、-5 D、-17. 某淘宝店家为迎接“双十一”抢购活动,在甲批发市场以每件a元的价格进了40件童装,又在乙批发市场以每件b元(a>b)的价格进了同样的60件童装.如果店家以每件 元的价格卖出这款童装,卖完后,这家商店( )A、盈利了 B、亏损了 C、不赢不亏 D、盈亏不能确定8. 实数 在数轴上的对应点的位置如图所示,下列关系式不成立的是( ) A、 B、 C、 D、9. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为 人,所列方程正确是( )A、 B、 C、 D、10. 我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为( )
A、 B、 C、 D、9. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为 人,所列方程正确是( )A、 B、 C、 D、10. 我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为( )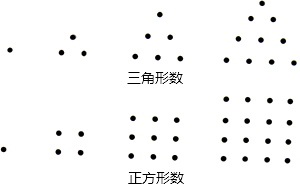 A、33 B、301 C、386 D、571
A、33 B、301 C、386 D、571二、填空题
-
11. ﹣3的相反数是 .12. 比较大小: .(填“<”,“=”或“>”)13. 已知关于x的方程2x+a+5=0的解是x=1,则a的值为 .14. 已知一个角的补角比这个角的一半多 ,则这个角的度数为.15. 已知 , , ,则 .16. 5个人围成一个圆圈做游戏,游戏的规则是:每个人心里都想好一个实数,并把自己想好的数如实地告诉他相邻的两个人,然后每个人将他相邻的两个人告诉他的数的平均数报出来.若报出来的数如图所示,则报4的人心里想的数是 .
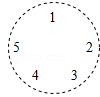
三、解答题
-
17. 解方程:(1)、 .(2)、18. 先化简,再求值:2(a2b+ab2)﹣3(a2b﹣1)﹣2ab2﹣4,其中a=2019,b= .19. 如图,已知四点A、B、C、D,用圆规和无刻度的直尺,按下列要求与步骤画出图形:
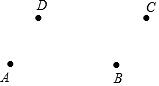 (1)、画直线AB;(2)、画射线DC;(3)、延长线段DA至点E,使AE=AB(保留作图痕迹)。20. 若 , ,且 .求 的值;21. 如图B、C两点把线段AD分成2:3:4三部分,M是AD的中点,CD=8,求MC的长.
(1)、画直线AB;(2)、画射线DC;(3)、延长线段DA至点E,使AE=AB(保留作图痕迹)。20. 若 , ,且 .求 的值;21. 如图B、C两点把线段AD分成2:3:4三部分,M是AD的中点,CD=8,求MC的长.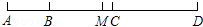 22. 阅读材料:我们知道,4x﹣2x+x=(4﹣2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
22. 阅读材料:我们知道,4x﹣2x+x=(4﹣2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.尝试应用:
(1)、把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2的结果是(2)、已知x2﹣2y=4,求3x2﹣6y﹣21的值;(3)、已知a﹣2b=3,2b﹣c=﹣5,c﹣d=10,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.23. 在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.(1)、七年级(2)班有男生、女生各多少人?(2)、要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?24. 如图,∠AOB的边OA上有一动点P,从距离O点18cm的点M处出发,沿线段MO,射线OB运动,速度为2cm/s;动点Q从点O出发,沿射线OB运动,速度为1cm/s.P、Q同时出发,设运动时间是t(s).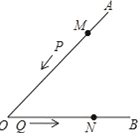 (1)、当点P在MO上运动时,PO=cm(用含t的代数式表示);(2)、当点P在MO上运动时,t为何值,能使OP=OQ?(3)、若点Q运动到距离O点16cm的点N处停止,在点Q停止运动前,点P能否追上点Q?如果能,求出t的值;如果不能,请说出理由.25. 学习千万条,思考第一条。请你用本学期所学知识探究以下问题:(1)、已知点 为直线 上一点,将直角三角板 的直角顶点放在点 处,并在 内部作射线 .
(1)、当点P在MO上运动时,PO=cm(用含t的代数式表示);(2)、当点P在MO上运动时,t为何值,能使OP=OQ?(3)、若点Q运动到距离O点16cm的点N处停止,在点Q停止运动前,点P能否追上点Q?如果能,求出t的值;如果不能,请说出理由.25. 学习千万条,思考第一条。请你用本学期所学知识探究以下问题:(1)、已知点 为直线 上一点,将直角三角板 的直角顶点放在点 处,并在 内部作射线 .①如图1,三角板的一边 与射线 重合,且 ,若以点 为观察中心,射线 表示正北方向,求射线 表示的方向;
②如图2,将三角板放置到如图位置,使 恰好平分 ,且 ,求 的度数.
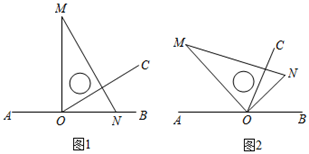 (2)、已知点 不在同一条直线上, , 平分 , 平分 ,用含 的式子表示 的大小.
(2)、已知点 不在同一条直线上, , 平分 , 平分 ,用含 的式子表示 的大小.