安徽省宣城市2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2020-02-27 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点A(5，6)与点B关于x轴对称，则点B的坐标为（）

A、(5，6) B、(－5，－6) C、(－5，6) D、(5，－6)

查看试题解析
2. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 已知点（-2，y₁），（-1，y₂），（1，y₃）都在直线y=－3x＋b上，则y₁ ， y₂ ， y₃的值的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{1} > y_{2} > y_{3}$ C、 $y_{3} > y_{1} > y_{2}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
4. 如图，△ABC中，AB＝AC，AD⊥BC，下列结论中错误的是（）

A、D是BC中点 B、AD平分∠BAC C、AB＝2BD D、∠B＝∠C

查看试题解析
5. 如图，在 $A B$ 、 $A C$ 上各取一点E、D，使 $A E = A D$ ，连接 $B D$ 、 $C E$ 相交于点O，再连接 $A O$ 、 $B C$ ，若 $∠ 1 = ∠ 2$ ，则图中全等三角形共有（）

A、2对 B、3对 C、4对 D、5对

查看试题解析
6. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D ⊥ B C$ ， $∠ B A D = 40 °$ ， $A D = A E$ ，则 $∠ C D E$ 的度数为（）

A、15° B、20° C、25° D、30°

查看试题解析
7. 等腰△ABC的周长为20，其中一边长为9，则这个等腰三角形的腰长为（　　）

A、5.5 B、9 C、11 D、5.5或9

查看试题解析
8. 下列结论正确是（）

A、两个锐角对应相等的两个直角三角形全等 B、命题“若 $a^{2} = b^{2}$ ，则 $a = b$ ”的逆命题是假命题 C、等腰三角形的高、中线、角平分线互相重合 D、角平分线上的点到这个角两边的距离相等

查看试题解析
9. 一次函数y=kx+b的图像经过点（ $m^{2} + 1$ ，1）和（-1， $m^{2} + 1$ ）（m≠0），则k、b应满足的条件是（）.

A、k＞0,b＞0 B、k＞0,b＜0 C、k＜0,b＜0 D、k＜0,b＞0

查看试题解析
10. 如图，已知线段AB=18米， $M A ⊥ A B$ 于点A，MA=6米，射线 $B D ⊥ A B$ 于点B，P点从B点出发向A运动，每秒走1米，Q点从B点向D点运动，每秒走2米，P，Q同时从B出发，则出发x秒后，在线段MA上有一点C，使△CAP与△PBQ全等，则x的值为（）

A、4 B、6 C、4或9 D、6或9

查看试题解析

二、填空题

11. 如图， $A B = C D$ ， $A D$ 与 $B C$ 交于点O，在不添加任何辅助线的前提下要使 $△ A O B ≌ △ C O D$ ，则需添加条件.

查看试题解析
12. 老师给出了一个函数，甲、乙两学生分别指出了这个函数的一个性质，甲：第二、四象限有它的图象；乙：在y轴上的截距为-2，请你写出一个能满足上述性质的函数关系式：.

查看试题解析
13. 已知一次函数y=（m-2）x+m-3的图像经过第一，第三，第四象限，则m的取值范围是．

查看试题解析
14. 如果 $y - m$ 与x成正比例，比例系数是2，且当 $x = 2$ 时， $y = 3$ ，则y与x的函数关系式为.

查看试题解析
15. 等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为．

查看试题解析
16. 如图，有一块边长为4的正方形塑料模板ABCD，将一块足够大的直角三角板的直角顶点落在A点，两条直角边分别与CD交于点F，与CB延长线交于点E．则四边形AECF的面积是．

查看试题解析
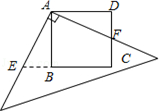17. 如图，在△ABC中， $∠ A B C = 45^{\circ} ， C D ⊥ A B 于点 D ， BE 平分 ∠ ABC ，$ 且 $BE ⊥ AC$ 于点E，与CD相交于点F， $DH ⊥ BC$ 于点H，交BE于点G.下列结论：①BD=CD；②AD+CF=BD；③ $C E = \frac{1}{2} B F$ ；④AE=CF.其中正确是（填序号）

查看试题解析

三、解答题

18.
如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）

(1)、请画出将△ABC向左平移4个单位长度后得到的图形△A₁B₁C₁；

(2)、请画出△ABC关于原点O成中心对称的图形△A₂B₂C₂；

(3)、在x轴上找一点P，使PA+PB的值最小，请直接写出点P的坐标．

查看试题解析
19. 如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连接AE、DE、DC。

(1)、求证：△ABE≌△CBD；

(2)、若∠CAE=30°，求∠BCD的度数。

查看试题解析
20. 如图，直线 $P A$ 是一次函数 $y = x + 1$ 的图象，直线 $P B$ 是一次函数 $y = - 2 x + 4$ 的图象.

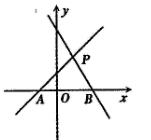(1)、求A、B、P三点坐标；

(2)、求 $△ P A B$ 的面积；

(3)、已知过P点的直线把 $△ P A B$ 分成面积相等的两部分，求该直线解析式.

查看试题解析
21. 在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑摩托车从B地到A地，到达A地后立即按原路返回．如图是甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：

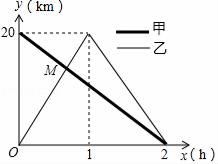(1)、直接写出y_甲， y_乙与x之间的函数关系式（不写过程）；

(2)、①求出点M的坐标，并解释该点坐标所表示的实际意义；②根据图象判断，x取何值时，y_乙＞y_甲．

查看试题解析
22. 问题情境：如图①，在△ABD与△CAE中，BD=AE，∠DBA=∠EAC，AB=AC，易证：△ABD≌△CAE．（不需要证明）

(1)、特例探究：如图②，在等边△ABC中，点D、E分别在边BC、AB上，且BD=AE，AD与CE交于点F．求证：△ABD≌△CAE．

(2)、归纳证明：如图③，在等边△ABC中，点D、E分别在边CB、BA的延长线上，且BD=AE．△ABD与△CAE是否全等？如果全等，请证明；如果不全等，请说明理由．

(3)、拓展应用：如图④，在等腰三角形中，AB=AC，点O是AB边的垂直平分线与AC的交点，点D、E分别在OB、BA的延长线上．若BD=AE，∠BAC=50°，∠AEC=32°，求∠BAD的度数．

查看试题解析