上海市金山区金山区教育局2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-27 类型:期末考试
一、单选题
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 下列一元二次方程中,有一个根为1的方程是( )A、 B、 C、 D、3. 已知正比例函 (k是常数, )中y随x的増大而增大,那么它和函数 (k是常数,k≠0)在同一平面直角坐标系内的大致图像可能是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列四组数据表示三角形的三边长,其中不能构成直角三角形的一组数据是( )A、1 cm, cm, 4cm B、5cm, 12cm, 13cm: C、3cm, 4cm, 5cm: D、7cm, 24cm, 25 cm5. 已知△ABC内一点M,如果点M到两边AB、BC的距离相等,那么点M( )A、在AC边的高上 B、在AC边的中线上 C、在∠ABC的平分线上 D、在AC边的垂直平分线上6. 下列四个命题:①有两边及其中一边的对角对应相等的两个三角形全等;②三角形的一条中线把三角形分成面积相等的两部分:③若 ,则 >0:④点P(1,2)关于原点的对称点坐标为P(-1,-2);其中真命题的是( )A、①、② B、②、④ C、③、④ D、①、③
4. 下列四组数据表示三角形的三边长,其中不能构成直角三角形的一组数据是( )A、1 cm, cm, 4cm B、5cm, 12cm, 13cm: C、3cm, 4cm, 5cm: D、7cm, 24cm, 25 cm5. 已知△ABC内一点M,如果点M到两边AB、BC的距离相等,那么点M( )A、在AC边的高上 B、在AC边的中线上 C、在∠ABC的平分线上 D、在AC边的垂直平分线上6. 下列四个命题:①有两边及其中一边的对角对应相等的两个三角形全等;②三角形的一条中线把三角形分成面积相等的两部分:③若 ,则 >0:④点P(1,2)关于原点的对称点坐标为P(-1,-2);其中真命题的是( )A、①、② B、②、④ C、③、④ D、①、③二、填空题
-
7. 化简: =8. 方程 的解为.9. 函数 的定义域是10. 已知函数 ,则 .11. 如果关于x的方程 (m为常数)有两个相等实数根,那么m= .12. 在实数范围内分解因式: .13. 已知点A(3,a)、B(-1,b)在函数 的图像上,那么ab(填“>”或“=”或“<”)14. 某小区2010年屋顶绿化面积为2000平方米,计划2012年屋顶绿化面积要达到2880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是.15. 命题“全等三角形的面积相等”的逆命题是16. 已知直角坐标平面内两点 和 ,则 、 两点间的距离等于 .17. 已知△ABC中,∠A=90°,角平分线BE、CF交于点O,则∠BOC= .18. 已知,在△ABC中,BC=3,∠A=22.5°,将△ABC翻折使得点B与点A重合,折痕与边AC交于点P,如果AP=4,那么AC的长为
三、解答题
-
19. 计算: .20. 解方程:21. 已知:y与2x-3成正比例,且当x=4时,y=10,求y与x的函数解析式22. 如图,在△ABC中,AC=BC,∠C=90∘,AD是△ABC的角平分线,DE⊥AB,垂足为E.求证:AB=AC+CD.
 23. 已知:△ABC中,AB=AC,∠BAC=120∘,
23. 已知:△ABC中,AB=AC,∠BAC=120∘,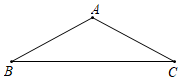 (1)、利用直尺、圆规,求作AB的垂直平分线DE,交BC于点D、交AB于点E:(不要求写出作法,但要求保留作图痕迹)(2)、若BD=3,求BC的长.24. 已知:如图,△ABC中,AD⊥BC,点D为垂足,AD=BD,点E在AD上,BE=AC
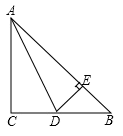
(1)、利用直尺、圆规,求作AB的垂直平分线DE,交BC于点D、交AB于点E:(不要求写出作法,但要求保留作图痕迹)(2)、若BD=3,求BC的长.24. 已知:如图,△ABC中,AD⊥BC,点D为垂足,AD=BD,点E在AD上,BE=AC (1)、求证:△BDE≌△ADC(2)、若M、N分别是BE、AC的中点,分别联结DM、DN. 求证:DM⊥DN
(1)、求证:△BDE≌△ADC(2)、若M、N分别是BE、AC的中点,分别联结DM、DN. 求证:DM⊥DN