福建省龙岩市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-27 类型:期末考试
一、单选题
-
1. ( )A、 B、 C、 D、2. 下列交通路口分流图案中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确是( )A、 B、 C、 D、4. 计算下列四个式子,其值大于 的是( )A、 B、 C、 D、5. 下列各组的分式不一定相等的是( )A、 与 B、 与 C、 与 D、 与6. , 两地相距 ,一艘轮船从 地逆流航行到 地,又立即从 地顺流航行到 地,共用去 ,已知水流速度为 ,若设该轮船在静水中的速度为 ,则下列所列方程正确是( )A、 B、 C、 D、7. 下列简写的全等三角形的判定定理中,与角没有关系的是( )A、SSS B、HL C、AAS D、SAS8. 在平面直角坐标系中,已知 , ,若点 在第一象限,且 为等腰直角三角形,则正确所有点 的 值之和是( )A、 B、 C、 D、9. 如图, , , ,若 ,则 ( )
3. 下列计算正确是( )A、 B、 C、 D、4. 计算下列四个式子,其值大于 的是( )A、 B、 C、 D、5. 下列各组的分式不一定相等的是( )A、 与 B、 与 C、 与 D、 与6. , 两地相距 ,一艘轮船从 地逆流航行到 地,又立即从 地顺流航行到 地,共用去 ,已知水流速度为 ,若设该轮船在静水中的速度为 ,则下列所列方程正确是( )A、 B、 C、 D、7. 下列简写的全等三角形的判定定理中,与角没有关系的是( )A、SSS B、HL C、AAS D、SAS8. 在平面直角坐标系中,已知 , ,若点 在第一象限,且 为等腰直角三角形,则正确所有点 的 值之和是( )A、 B、 C、 D、9. 如图, , , ,若 ,则 ( )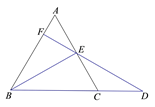 A、 B、 C、 D、10. 如图, 中, 的垂直平分线 交 的平分线 于点 ,过 作 于点 ,若 , ,则 ( )
A、 B、 C、 D、10. 如图, 中, 的垂直平分线 交 的平分线 于点 ,过 作 于点 ,若 , ,则 ( )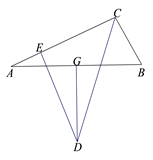 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
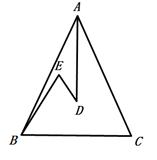
11. 因式分解: ;12. 计算: ;13. 方程 的解是;14. 一组按规律排列的式子: , , , ,( ),其中第10个式子是;15. 若正 边形的内角和与其中一个外角的和为 ,则 =;16. 如图,已知 , 平分 , ,若 , ,则 = .
三、解答题
-
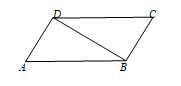
17. 计算:18. 解方程: .19. 先化简,后求值: ,其中 .20. 如图, ∥ , .求证: .
 21. 已知 , , .(1)、当 , , 时,求 的值;(2)、当 时,求 的值.22. 在我国南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,用下图的三角形解释二项和的乘方规律.杨辉在注释中提到,在他之前北宋数学家贾宪(1050年左右)也用过上述方法,因此我们称这个三角形为“杨辉三角”或“贾宪三角”.杨辉三角两腰上的数都是 ,其余每一个数为它上方(左右)两数的和.事实上,这个三角形给出了 的展开式(按 的次数由大到小的顺序)的系数规律.例如,此三角形中第三行的 个数 ,恰好对应着 展开式中的各项系数,第四行的 个数 ,恰好对应着 展开式中的各项系数,等等.请依据上面介绍的数学知识,解决下列问题:
21. 已知 , , .(1)、当 , , 时,求 的值;(2)、当 时,求 的值.22. 在我国南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,用下图的三角形解释二项和的乘方规律.杨辉在注释中提到,在他之前北宋数学家贾宪(1050年左右)也用过上述方法,因此我们称这个三角形为“杨辉三角”或“贾宪三角”.杨辉三角两腰上的数都是 ,其余每一个数为它上方(左右)两数的和.事实上,这个三角形给出了 的展开式(按 的次数由大到小的顺序)的系数规律.例如,此三角形中第三行的 个数 ,恰好对应着 展开式中的各项系数,第四行的 个数 ,恰好对应着 展开式中的各项系数,等等.请依据上面介绍的数学知识,解决下列问题: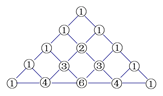 (1)、写出 的展开式;(2)、利用整式的乘法验证你的结论.23. 如图,射线 的端点 是线段 的中点,请根据下列要求作答:
(1)、写出 的展开式;(2)、利用整式的乘法验证你的结论.23. 如图,射线 的端点 是线段 的中点,请根据下列要求作答: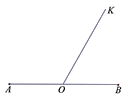 (1)、尺规作图:在射线 上作点 ,连接 ,使 > ;(2)、利用(1)中你所作的图,求证: .
(1)、尺规作图:在射线 上作点 ,连接 ,使 > ;(2)、利用(1)中你所作的图,求证: .