北京市石景山区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-27 类型:期末考试
一、单选题
-
1. 2的平方根为( )A、4 B、±4 C、 D、±2. 下列照片分别是新首钢大桥、大兴机场、中国尊、丽泽夜空之眼,照片中主体建筑的 平面图形不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列说法正确是( )A、可能性很大的事件在一次试验中一定发生 B、可能性很大的事件在一次试验中不一定会发生 C、必然事件在一次试验中有可能不会发生 D、不可能事件在一次试验中也可能发生4. 使得分式 有意义的 m 的取值范围是( )A、m≠0 B、m≠2 C、m≠-3 D、m>-35. 下列各式中,运算正确是( )A、 B、 C、 D、6. 若最简二次根式 与最简二次根式 是同类二次根式,则x的值为( )A、x=0 B、x=1 C、x=2 D、x=-27. 如图,△ABC中,AB =AC,过点A作DA⊥AC交BC于点 D .若∠B=2∠BAD,则∠BAD的度数为( )
3. 下列说法正确是( )A、可能性很大的事件在一次试验中一定发生 B、可能性很大的事件在一次试验中不一定会发生 C、必然事件在一次试验中有可能不会发生 D、不可能事件在一次试验中也可能发生4. 使得分式 有意义的 m 的取值范围是( )A、m≠0 B、m≠2 C、m≠-3 D、m>-35. 下列各式中,运算正确是( )A、 B、 C、 D、6. 若最简二次根式 与最简二次根式 是同类二次根式,则x的值为( )A、x=0 B、x=1 C、x=2 D、x=-27. 如图,△ABC中,AB =AC,过点A作DA⊥AC交BC于点 D .若∠B=2∠BAD,则∠BAD的度数为( )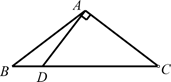 A、18° B、20° C、30° D、36°8. 如图,已知∠O ,点 P 为其内一定点,分别在∠O 的两边上找点 A 、 B ,使△ PAB 周长最小的是( )A、.
A、18° B、20° C、30° D、36°8. 如图,已知∠O ,点 P 为其内一定点,分别在∠O 的两边上找点 A 、 B ,使△ PAB 周长最小的是( )A、.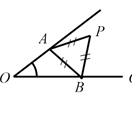 B、
B、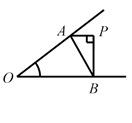 C、
C、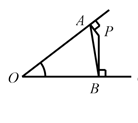 D、
D、
二、填空题
-
9. 写出一个满足 的整数a的值为:.10. 下面是小军同学计算 的过程:
=
=
=
=
=
其中运算步骤[2]为: , 该步骤的依据是 .
11. 如果等腰三角形的一个角比另一个角大30° ,那么它的顶角是度12. 用一组 a , b 的值说明式 是错误的,这组值可以是a= , b=13. 桌子上有6杯同样型号的杯子,其中1杯白糖水,2杯矿泉水,3杯凉白开,从6个杯子中随机取出1杯,请你将下列事件发生的可能性从大到小排列: .(填序号即可)①取到凉白开 ②取到白糖水 ③取到矿泉水 ④没有取到矿泉水14. 如图,三角形纸片 ABC 中, ∠ACB = 90o , BC = 6 , AB = 10 .在 AC 边上取一点 E , 以 BE 为折痕,使 AB 的一部分与 BC 重合, A 与 BC 延长线上的点 D 重合,则CE 的长 为 .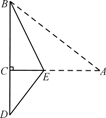 15. 对于任意不相等的两个实数 a、b,定义运算
15. 对于任意不相等的两个实数 a、b,定义运算 如下: ,如 ,那么8
如下: ,如 ,那么8 12的运算结果为 .
12的运算结果为 .
16. 如图,△OAB是腰长为1的等腰直角三角形,∠OAB=90°,延长OA至B1 , 使AB1=OA,以OB1为底,在△OAB外侧作等腰直角三角形OA1B1 , 再延长OA1至B2 , 使A1B2=OA1 , 以OB2为底,在△OA1B1外侧作等腰直角三角形OA2B2 , ……,按此规律作等腰直角三角形OAnBn(n≥1,n为正整数),回答下列问题:
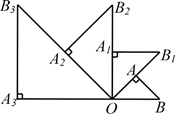 (1)、A3B3的长是;(2)、△OA2020B2020的面积是.
(1)、A3B3的长是;(2)、△OA2020B2020的面积是.三、解答题
-
17. 计算:18. 计算:19. 解方程:20. 已知: ,求代数式 的值.21. 如图,在4´4的正方形网格中,有5个黑色小正方形.
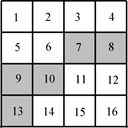 (1)、请你移动一个黑色小正方形,使移动后所形成的4´4的正方形网格图形是轴对称图形.如:将8号小正方形移至14号;你的另一种做法是将号小正方形移至号(填写标号即可);(2)、请你移动2个小正方形,使移动后所形成的图形是轴对称图形.你的一种做法是将号小正方形移至号、将号小正方形移至号(填写标号即可).22. 已知:如图,AB=AE.∠C=∠F,∠EAC=∠BAF.求证:AC=AF.
(1)、请你移动一个黑色小正方形,使移动后所形成的4´4的正方形网格图形是轴对称图形.如:将8号小正方形移至14号;你的另一种做法是将号小正方形移至号(填写标号即可);(2)、请你移动2个小正方形,使移动后所形成的图形是轴对称图形.你的一种做法是将号小正方形移至号、将号小正方形移至号(填写标号即可).22. 已知:如图,AB=AE.∠C=∠F,∠EAC=∠BAF.求证:AC=AF. 23. 下面是小明同学设计的“已知底边及底边上的中线作等腰三角形”的尺规作图过程.
23. 下面是小明同学设计的“已知底边及底边上的中线作等腰三角形”的尺规作图过程.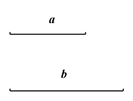
已知:如图1,线段a和线段b.
求作:△ABC,使得AB=AC,BC=a,BC边上的中线为b.
作法:如图,

①作射线BM,并在射线BM上截取BC=a;
②作线段BC的垂直平分线PQ,PQ交BC于D;
③以D为圆心,b为半径作弧,交PQ于A;
④连接AB和AC.
则△ABC为所求作的图形.
根据上述作图过程,回答问题:
(1)、用直尺和圆规,补全图2中的图形;(2)、完成下面的证明:证明:由作图可知BC=a,AD=b.
∵PQ为线段BC的垂直平分线,点A在PQ上,
∴AB=AC(填依据).
又∵线段BC的垂直平分线PQ交BC于D,
∴BD=CD.(填依据).
∴AD为BC边上的中线,且AD=b.
24. 甲、乙两个施工队共同完成某区域绿化改造工程,乙队先单独做3天后,再由两队合作7天完成全部工程.已知乙队单独完成此项工程所需天数是甲队单独完成此项工程所需天数的2倍,求甲、乙两个施工队单独完成此项工程各需多少天?25. 如图,△ABC中, ,且AD=AC.若∠ABC=45°,D是BC边上一点,BD-DC=1.求DC的长.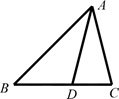 26. 已知:如图△ABC,直线l.求作:点P.使得点P在直线l上,且点P、点A、点B构成的三角形为等腰三角形(保留作图痕迹,不必写出作法).
26. 已知:如图△ABC,直线l.求作:点P.使得点P在直线l上,且点P、点A、点B构成的三角形为等腰三角形(保留作图痕迹,不必写出作法).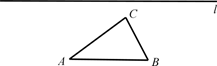
解:
(1)、满足条件的点共有个;(2)、在图中用尺规作图作出满足条件的点P(保留作图痕迹,不必写出作法).27. 我们知道,假分数可以化为整数与真分数的和的形式.例如:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
例如:像 , …,这样的分式是假分式;像 , …,这样
的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式.
解决下列问题:
(1)、将分式 化为整式与真分式的和的形式为:.(直接写出结果即可)(2)、如果 的值为整数,求x的整数值.28. 如图,在等边△ABC中,点D是线段BC上一点.作射线AD,点B关于射线AD的对称点为E.连接EC并延长,交射线AD于点F.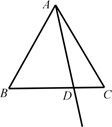 (1)、补全图形;(2)、求∠AFE的度数;(3)、用等式表示线段AF、CF、EF之间的数量关系,并证明.
(1)、补全图形;(2)、求∠AFE的度数;(3)、用等式表示线段AF、CF、EF之间的数量关系,并证明.