广东省汕头市潮南区两英镇2019-2020学年九年级上学期数学期末考试试卷
试卷更新日期:2020-02-27 类型:期末考试
一、单选题
-
1. 抛物线y=﹣ x2的顶点坐标是( )A、(0, ) B、(0, ) C、(0,0) D、(1,﹣ )2. 已知一元二次方程x2+kx﹣5=0有一个根为1,k的值为( )A、﹣2 B、2 C、﹣4 D、43. 下列图形:(1)等边三角形,(2)矩形,(3)平行四边形,(4)菱形,是中心对称图形的有( )个A、4 B、3 C、2 D、14. 抛掷一枚质地均匀的硬币,正面朝上的概率为0.5,下列说法正确是( )A、连续抛掷2次必有1次正面朝上 B、连续抛掷10次不可能都正面朝上 C、大量反复抛掷每100次出现正面朝上50次 D、通过抛掷硬币确定谁先发球的比赛规则是公平的5. 已知A为⊙O外一点,若点A到⊙O上的点的最短距离为2,最长离为4,则⊙O半径为( )A、4 B、3 C、2 D、16. 在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外完全相同,其中有5个黄球,4个蓝球.若随机摸出一个蓝球的概率为 ,则随机摸出一个红球的概率为( )A、 B、 C、 D、7. 如图,将△AOB绕点O按逆时针方向旋转 后得到△COD,若 ,则 的度数是( )
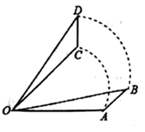 A、 B、 C、 D、8. 我们知道方程x2+2x﹣3=0的解是x1=1,x2=﹣3,现给出另一个方程(2x+3)2+2(2x+3)﹣3=0,它的解是( )A、x1=1,x2=3 B、x1=1,x2=﹣3 C、x1=﹣1,x2=3 D、x1=﹣1,x2=﹣39. 抛物线y=﹣x2+2x﹣2与坐标轴的交点个数为( )A、0 B、1 C、2 D、310. 如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为5,CD=8,则弦AC的长为( )
A、 B、 C、 D、8. 我们知道方程x2+2x﹣3=0的解是x1=1,x2=﹣3,现给出另一个方程(2x+3)2+2(2x+3)﹣3=0,它的解是( )A、x1=1,x2=3 B、x1=1,x2=﹣3 C、x1=﹣1,x2=3 D、x1=﹣1,x2=﹣39. 抛物线y=﹣x2+2x﹣2与坐标轴的交点个数为( )A、0 B、1 C、2 D、310. 如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为5,CD=8,则弦AC的长为( )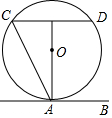 A、10 B、8 C、4 D、4
A、10 B、8 C、4 D、4二、填空题
-
11. 若点P(﹣2,b)与点M(a,3)关于原点对称,则a+b= .12. 有四张看上去无差别的卡片,正面分别写有“兴城首山”、“龙回头”、“觉华岛”、“葫芦山庄”四个景区的名称,将它们背面朝上,从中随机一张卡片正面写有“葫芦山庄”的概率是 .
13. 若x2+3x=0,则2019﹣2x2﹣6x的值为 .14. 如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,AB=8,则 的长为 .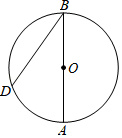 15. 如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a﹣b+c的值为 .
15. 如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a﹣b+c的值为 .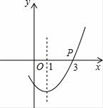 16. 如图,将△ABC沿BC翻折得到△DBC,再将△DBC绕C点逆时针旋转60°得到△FEC,延长BD交EF于H,已知∠ABC=30°,∠BAC=90°,AC=1,则四边形CDHF的面积为 .
16. 如图,将△ABC沿BC翻折得到△DBC,再将△DBC绕C点逆时针旋转60°得到△FEC,延长BD交EF于H,已知∠ABC=30°,∠BAC=90°,AC=1,则四边形CDHF的面积为 .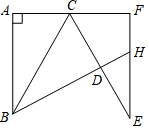 17. 这样铺地板:第一块铺2块,如图1,第二次把第一次的完全围起来,如图2;第三次把第二次的完全围起来,如图3;…依次方法,铺第5次时需用木块才能把第四次所铺的完全围起来.
17. 这样铺地板:第一块铺2块,如图1,第二次把第一次的完全围起来,如图2;第三次把第二次的完全围起来,如图3;…依次方法,铺第5次时需用木块才能把第四次所铺的完全围起来.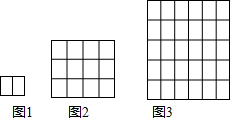
三、解答题
-
18. 解方程:(x﹣1)2=4.19. 已知:在△ABC中,AB=AC.
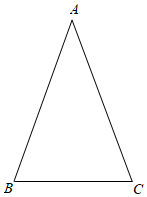 (1)、求作:△ABC的外接圆,圆心为O.(要求:尺规作图,保留作图痕迹,不写作法)(2)、若△ABC的外接圆的圆心O到BC边的距离为4,BC=6,则⊙O的半径长为 .20. 剪纸是中国传统的民间艺术,它画面精美,风格独特,深受大家喜爱,现有三张不透明的卡片,其中两张卡片的正面图案为“金鱼”,另外一张卡片的正面图案为“蝴蝶”,卡片除正面剪纸图案不同外,其余均相同.将这三张卡片背面向上洗匀从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求抽出的两张卡片上的图案都是“金鱼”的概率.(图案为“金鱼”的两张卡片分别记为A1、A2 , 图案为“蝴蝶”的卡片记为B)
(1)、求作:△ABC的外接圆,圆心为O.(要求:尺规作图,保留作图痕迹,不写作法)(2)、若△ABC的外接圆的圆心O到BC边的距离为4,BC=6,则⊙O的半径长为 .20. 剪纸是中国传统的民间艺术,它画面精美,风格独特,深受大家喜爱,现有三张不透明的卡片,其中两张卡片的正面图案为“金鱼”,另外一张卡片的正面图案为“蝴蝶”,卡片除正面剪纸图案不同外,其余均相同.将这三张卡片背面向上洗匀从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求抽出的两张卡片上的图案都是“金鱼”的概率.(图案为“金鱼”的两张卡片分别记为A1、A2 , 图案为“蝴蝶”的卡片记为B) 21. 已知关于x的一元二次方程x2﹣mx﹣2=0…①(1)、若x=﹣1是方程①的一个根,求m的值和方程①的另一根;(2)、对于任意实数m , 判断方程①的根的情况,并说明理由.22. 在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度 得到△AED , 点B、C的对应点分别是E、D.
21. 已知关于x的一元二次方程x2﹣mx﹣2=0…①(1)、若x=﹣1是方程①的一个根,求m的值和方程①的另一根;(2)、对于任意实数m , 判断方程①的根的情况,并说明理由.22. 在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度 得到△AED , 点B、C的对应点分别是E、D.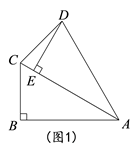
 (1)、如图1,当点E恰好在AC上时,求∠CDE的度数;(2)、如图2,若 =60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.23. 工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)
(1)、如图1,当点E恰好在AC上时,求∠CDE的度数;(2)、如图2,若 =60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.23. 工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计) (1)、在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?(2)、若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?24. 如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
(1)、在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?(2)、若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?24. 如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.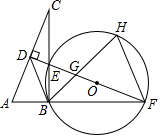 (1)、试判断BD与⊙O的位置关系,并说明理由;(2)、当AB=BE=1时,求⊙O的面积;(3)、在(2)的条件下,求HG的长.25. 如图,在直角坐标系xOy中,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.
(1)、试判断BD与⊙O的位置关系,并说明理由;(2)、当AB=BE=1时,求⊙O的面积;(3)、在(2)的条件下,求HG的长.25. 如图,在直角坐标系xOy中,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.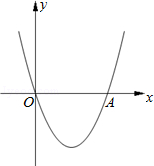 (1)、求这个二次函数的解析式;(2)、在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;(3)、对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由.
(1)、求这个二次函数的解析式;(2)、在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;(3)、对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由.