福建省福州市鼓楼区2019-2020学年九年级上学期数学期末考试试卷
试卷更新日期：2020-02-27 类型：期末考试
一、单选题
-
1. 下列电动车品牌标志中，既是轴对称图形，又是中心对称图形的是（ ）A、
B、
C、
D、
2. “2020年的6月21日是晴天”这个事件是（ ）A、确定事件 B、不可能事件 C、必然事件 D、不确定事件3. 点P（﹣2019，2020）关于原点的对称点P′在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 在一张复印出来的纸上，一个三角形的一条边由原图中的2cm变成了6cm，则复印出的三角形的面积是原图中三角形面积的（ ）A、3倍 B、6倍 C、9倍 D、12倍5. 《孙子算经》是我国古代重要的数学著作，其下卷有题如下：“今有竿不知长短，度其影得一丈五尺．别立一表，长一尺五寸，影得五寸．问竿长几何？”译文：“有一根竹竿不知道它的长短，量出它在太阳下的影子长一丈五尺．同时立一根一尺五寸的小标杆，它的影长是五寸，则这根竹竿的长度为多少尺？”可得这根竹竿的长度为（ ）（提示： 丈 尺， 尺 寸）
A、五丈 B、四丈五尺 C、五尺 D、四尺五寸6. 如图，BC是半圆O的直径，D ， E是 上两点，连接BD ， CE并延长交于点A ， 连接OD ， OE ， 如果 ，那么 的度数为（ ）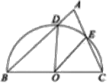
A、35° B、40° C、60° D、70°7. 二次函数y＝﹣3（x+1）2﹣7有（ ）A、最大值﹣7 B、最小值﹣7 C、最大值7 D、最小值78. 若关于x的一元二次方程ax2+bx+5＝0的一个根是x＝﹣1，则2015﹣a+b的值是（ ）A、2012 B、2016 C、2020 D、20219. 如图，点A是反比例图数y＝ （x＜0）图象上一点，AC⊥x轴于点C，与反比例函数y＝ （x＜0）图象交于点B，AB＝2BC，连接OA、OB，若△OAB的面积为3，则m+n＝（ ）
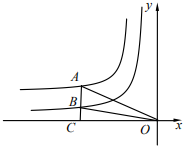A、﹣4 B、﹣6 C、﹣8 D、﹣1210. 已知非负数a，b，c满足a+b＝2，c﹣3a＝4，设S＝a2+b+c的最大值为m，最小值为n，则m﹣n的值为（ ）A、9 B、8 C、1 D、二、填空题
-
11. 抛物线y＝x2﹣4x的对称轴为直线 ．12. 如图，飞镖游戏板中每一块小正方形除颜色外都相同．若某人向游戏板投掷飞镖一次（假设飞镖落在游戏板上），则飞镖落在阴影部分的概率是.
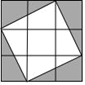13. 一个扇形的面积为6π，半径为4，则此扇形的圆心角为°．14. 已知 是方程 的根，则式子 ；15. 准备在一块长为30米，宽为24米的长方形花圃内修建四条宽度相等，且与各边垂直的小路，(如图所示)四条小路围成的中间部分恰好是一个正方形，且边长是小路宽度的4倍，若四条小路所占面积为80平方米，则小路的宽度为米 .
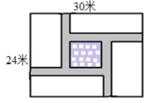16. 如图，半圆的圆心与坐标原点重合，半圆的半径1，直线 的解析式为 若直线 与半圆只有一个交点，则t的取值范围是 ．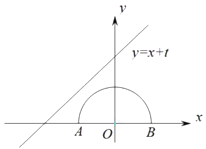
三、解答题
-
17. (用配方法解一元二次方程)： + -1=018. 已知二次函数y＝x2+2x+a﹣2的图象和x轴有两个交点．(1)、求实数a的取值范围；(2)、在（1）的前提下，a取最大整数值时，求这个二次函数图象的顶点坐标．19. “特色福州，美好生活”，福州举行金色秋天旅游活动．明明和华华同学分析网上关于旅游活动的信息，发现最具特色的景点有：①鼓岭、②森林公园、③青云山．他们准备周日下午去参观游览，各自在这三中个景点任选一个，每个景点被选中的可能性相同．(1)、明明同学在三个备选景点中选中鼓岭的概率是 ．(2)、用树状图或列表法求出明明和华华他们选中不同景点参观的概率是多少？20. 如图，AB是⊙O的直径，射线BC交⊙O于点D，E是劣弧AD上一点，且 ，过点E作EF⊥BC于点F，延长FE和BA的延长线交与点G．
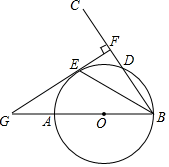(1)、证明：GF是⊙O的切线；(2)、若AG＝6，GE＝6 ，求△GOE的面积．21. 如图，P是等边三角形ABC内的一点，且PA＝6，PB＝8，PC＝10．
(1)、尺规作图：作出将△PAC绕点A逆时针旋转60°后所得到的△P′AB（不要求写作法，但需保留作图痕迹）．(2)、求点P与点P′之间的距离及∠APB的度数．22. 如图，∠ABD＝∠BCD＝90°，AB•CD＝BC•BD，BM∥CD交AD于点M．连接CM交DB于点N．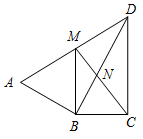
(1)、求证：△ABD∽△BCD；(2)、若CD＝6，AD＝8，求MC的长．23. 如图，已知点A在反比例函数 （x＞0）的图像上，过点A作AC⊥x轴，垂足是C，AC=OC．一次函数y=kx+b的图像经过点A，与y轴的正半轴交于点B．
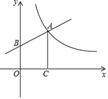(1)、求点A的坐标；(2)、若四边形ABOC的面积是 ，求一次函数y=kx+b的表达式．24. 如图，在△ABC中，∠BAC＝90°，点F在BC边上，过A，B，F三点的⊙O交AC于另一点D，作直径AE，连结EF并延长交AC于点G，连结BE，BD，四边形BDGE是平行四边形．
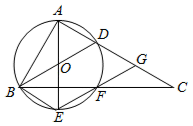(1)、求证：AB＝BF．(2)、当F为BC的中点，且AC＝3时，求⊙O的直径长．25. 如图①抛物线y＝ax2+bx+3（a≠0）与x轴，y轴分别交于点A（﹣1，0），B（3，0），点C三点．
(1)、试求抛物线的解析式；(2)、点D（2，m）在第一象限的抛物线上，连接BC，BD．试问，在对称轴左侧的抛物线上是否存在一点P，满足∠PBC＝∠DBC？如果存在，请求出点P点的坐标；如果不存在，请说明理由；(3)、点N在抛物线的对称轴上，点M在抛物线上，当以M、N、B、C为顶点的四边形是平行四边形时，请直接写出点M的坐标．