安徽省六安市七校联2018-2019学年九年级上学期数学期末考试试卷

试卷更新日期：2020-02-27 类型：期末考试

进入出卷网下载

一、单选题

1. 在△ABC中，若三边BC、CA、AB满足 BC∶CA∶AB=5∶12∶13，则cosB=（）

A、 $\frac{5}{12}$ B、 $\frac{12}{5}$ C、 $\frac{5}{13}$ D、 $\frac{12}{13}$

查看试题解析
2. 如果两个相似三角形的面积比是1：2，那么它们的周长比是（　　）

A、1：4 B、1： $\sqrt{2}$ C、 $\sqrt{2}$ ：1 D、4：1

查看试题解析
3. 抛物线y=x²的图象向左平移2个单位，再向下平移1个单位，则所得抛物线的解析式为（　　）

A、 $y = x^{2} + 4 x + 3$ B、 $y = x^{2} + 4 x + 5$ C、 $y = x^{2} - 4 x + 3$ D、 $y = x^{2} - 4 x - 5$

查看试题解析
4. 如图，不能判定△AOB和△DOC相似的条件是（）

A、AO•CO=BO•DO B、 $\frac{A O}{D O} = \frac{A B}{C D}$ C、∠A=∠D D、∠B=∠C

查看试题解析
5. 如图， $△ A B C$ 中，点 $D$ 在线段 $A B$ 上，且 $∠ B A D = ∠ C$ ，则下列结论一定正确是（）

A、 $A B^{2} = A C \cdot B D$ B、 $A B \cdot A D = B D \cdot B C$ C、 $A B^{2} = B C \cdot B D$ D、 $A B \cdot A D = B D \cdot C D$

查看试题解析
6. 在Rt△ABC中，∠C=90°，下列式子中不一定成立的是（）

A、tanA= $\frac{sin A}{cos A}$ B、sin²A+sin²B=1 C、sin²A+cos²A=1 D、sinA=sinB

查看试题解析
7. 如图，在△ABC中，CD平分∠ACB，过D作BC的平行线交AC于点M，那么 $\frac{B D}{A B}$ ＝（　　）

A、 $\frac{DM}{AC}$ B、 $\frac{DM}{BC}$ C、 $\frac{CM}{DM}$ D、 $\frac{C M}{A M}$

查看试题解析
8. 如图是二次函数y＝ax²+bx+c的部分图象，由图象可知不等式ax²+bx+c＜0的解集是（　　）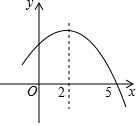

A、﹣1＜x＜5 B、x＞5 C、﹣1＜x且x＞5 D、x＜﹣1或x＞5

查看试题解析
9.
如图，正方形ABCD的边长为1，E、F分别是边BC和CD上的动点（不与正方形的顶点重合），不管E、F怎样动，始终保持AE⊥EF ．设BE=x ， DF=y ，则y是x的函数，函数关系式是（　　）

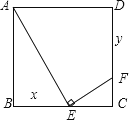A、y=x+1 B、y=x-1 C、y=x²-x+1 D、y=x²-x-1

查看试题解析
10. 如图所示，一般书本的纸张是在原纸张多次对开得到的.矩形 $A B C D$ 沿 $E F$ 对开后，再把矩形 $E F C D$ 沿 $M N$ 对开，依此类推.若各种开本的矩形都相似，那么 $\frac{A B}{A D}$ 等于（）.

A、 $0.618$ B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、 $2$

查看试题解析

二、填空题

11. 已知α为锐角,且sin (90°-α)= $\frac{\sqrt{3}}{2}$ ,则cosα=.

查看试题解析
12. 已知 $\frac{a}{2} = \frac{b}{3} = \frac{c}{4}$ ，则 $\frac{2 a - b + 3 c}{3 a - 2 b + c}$ ＝．

查看试题解析
13. 如图，在正方形网格中，∠1+∠2+∠3＝度．

查看试题解析
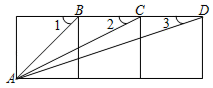14.
如图，在△ABC中，∠B=90°，AB=12mm ， BC=24mm ，动点P从点A开始沿边AB向B以2mm/s的速度移动（不与点B重合），动点Q从点B开始沿边BC向C以4mm/s的速度移动（不与点C重合）．如果P、Q分别从A、B同时出发，那么经过秒，四边形APQC的面积最小．

查看试题解析

三、解答题

15. 计算：cos²30°+sin²45°﹣tan60°•tan30°

查看试题解析
16. 如图，某飞机于空中A处测得目标C，此时高度AC＝1200米，从飞机上看到指挥所B的俯角为30°，求飞机A与指挥所B之间的距离．

查看试题解析
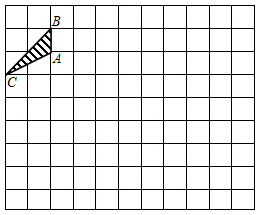
17. 如图，以点O为位似中心，在网格内将△ABC放大2倍得到△A′B′C′，若A点坐标为
（﹣1，1）．请写出A′点的坐标．

查看试题解析
18. 已知抛物线 $y = - \frac{1}{2} x^{2} - x + 4$ ，则：

(1)、x取何范围时，y随x增大而减小？

(2)、x取何范围时，抛物线在x轴上方？

查看试题解析
19. 阿静家在新建的楼房旁围成一个矩形花圃，花圃的一边利用20米长的院墙，另三边用总长为32米的离笆恰好围成．如图，设AB边的长为x米，矩形ABCD的面积为S平方米．

(1)、求S与x之间的函数关系式，并写出自变量x的取值范围．

(2)、当x为何值时，S有最大值？并求出最大值．

查看试题解析
20. 如图，已知一次函数 $y_{1} = k x - 2$ 的图象与反比例函数 $y_{2} = \frac{m}{x} (x > 0)$ 的图象交于 $A$ 点，与 $x$ 轴、 $y$ 轴交于 $C ， D$ 两点，过 $A$ 作 $A B$ 垂直于 $x$ 轴于 $B$ 点.已知 $A B = 1 ， B C = 2$ .

(1)、求一次函数 $y_{1} = k x - 2$ 和反比例函数 $y_{2} = \frac{m}{x} (x > 0)$ 的表达式；

(2)、观察图象：当 $x > 0$ 时，比较 $y_{1} ， y_{2}$ .

查看试题解析
21. 如图，在一笔直的海岸线L上有A、B两个观测点，A在B的正东方向，AB＝2km．有一艘小船在点P处，从A处测得小船在北偏西60°的方向，从B处测得小船在北偏东45°方向．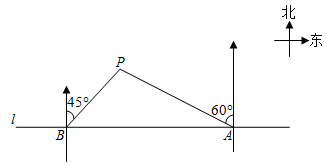

(1)、求P点到海岸线l的距离．

(2)、小船从点P处沿射线AP的方向继续行驶，求小船到B处的最短距离．

查看试题解析
22. 如图，在Rt△ABC中，∠C=90°，翻折∠C，使点C落在斜边AB上某一点D处，折痕为EF（点E、F分别在边AC、BC上）

(1)、若△CEF与△ABC相似．
①当AC=BC=2时，AD的长为；

②当AC=3，BC=4时，AD的长为；

(2)、当点D是AB的中点时，△CEF与△ABC相似吗？请说明理由．

查看试题解析
23. 已知抛物线y＝ax²＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．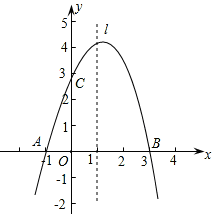

(1)、求抛物线的函数关系式；

(2)、设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；

(3)、在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．

查看试题解析