浙教版备考2020年中考数学一轮专题13 综合复习
试卷更新日期:2020-02-27 类型:一轮复习
一、选择题
-
1. 下列事件是必然事件的是( )A、明天要下雨; B、打开电视机,正在直播足球比赛; C、抛掷一枚正方体骰子,掷得的点数不会小于1; D、买一张彩票,一定会中一等奖.2. 如图是由三个相同小正方体组成的几何体的主视图,那么这个几何体可以是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 在同一平面直角坐标系中,一次函数 与二次函数 的图象大致为( )A、
3. 在同一平面直角坐标系中,一次函数 与二次函数 的图象大致为( )A、 B、
B、 C、
C、 D、
D、 4. 已知:如图,四边形ABCD是⊙O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是( )
4. 已知:如图,四边形ABCD是⊙O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是( )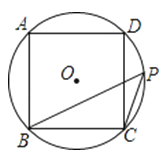 A、45° B、60° C、75° D、90°5.
A、45° B、60° C、75° D、90°5.如图,AB是⊙O的弦,AC是⊙O切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )
 A、20° B、25° C、40° D、50°6. 如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=( )
A、20° B、25° C、40° D、50°6. 如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=( ) A、60° B、65° C、72° D、75°7. 如图,直线l1∥l2∥l3 , 直线AC分别交l1 , l2 , l3于点A,B,C,直线DF分别交l1 , l2 , l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则 的值为( )
A、60° B、65° C、72° D、75°7. 如图,直线l1∥l2∥l3 , 直线AC分别交l1 , l2 , l3于点A,B,C,直线DF分别交l1 , l2 , l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则 的值为( ) A、 B、2 C、 D、8. 如图,点E在正方形ABCD的CD边上,连结BE,将正方形折叠,使点B与E重合, 折痕MN交BC边于点M,交AD边于点N,若tan∠EMC= ,ME+CE=8,则折痕MN的长为( )
A、 B、2 C、 D、8. 如图,点E在正方形ABCD的CD边上,连结BE,将正方形折叠,使点B与E重合, 折痕MN交BC边于点M,交AD边于点N,若tan∠EMC= ,ME+CE=8,则折痕MN的长为( ) A、 B、4 C、3 D、139. 如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( )
A、 B、4 C、3 D、139. 如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( )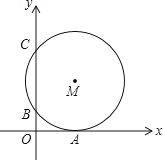 A、10 B、8 C、4 D、210. 将抛物线y=﹣2x2+1向右平移1个单位,再向上平移2个单位后所得到的抛物线为( )A、y=﹣2(x+1)2﹣1 B、y=﹣2(x+1)2+3 C、y=﹣2(x﹣1)2﹣1 D、y=﹣2(x﹣1)2+311. 已知二次函数y=(x+m)2–n的图象如图所示,则一次函数y=mx+n与反比例函数y= 的图象可能是( )
A、10 B、8 C、4 D、210. 将抛物线y=﹣2x2+1向右平移1个单位,再向上平移2个单位后所得到的抛物线为( )A、y=﹣2(x+1)2﹣1 B、y=﹣2(x+1)2+3 C、y=﹣2(x﹣1)2﹣1 D、y=﹣2(x﹣1)2+311. 已知二次函数y=(x+m)2–n的图象如图所示,则一次函数y=mx+n与反比例函数y= 的图象可能是( )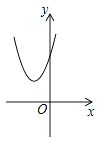 A、
A、 B、
B、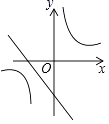 C、
C、 D、
D、 12. 二次函数的部分图象如图所示,对称轴是 ,则这个二次函数的表达式为( )
12. 二次函数的部分图象如图所示,对称轴是 ,则这个二次函数的表达式为( )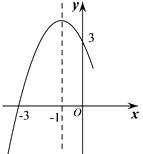 A、 B、 C、 D、13.
A、 B、 C、 D、13.函数y=x2+bx+c与y=x的图像如图所示,有以下结论:
①b2﹣4c>0;
②b+c+1=0;
③3b+c+6=0;
④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
 A、1个 B、2个 C、3个 D、4个14. 如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥AC∥HG,EH∥BD∥FG,则四边形EFGH的周长是( )
A、1个 B、2个 C、3个 D、4个14. 如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥AC∥HG,EH∥BD∥FG,则四边形EFGH的周长是( ) A、 B、13 C、 D、15. 一个立方体的每一个面都写有一个自然数,并且相对的两个面内的两数之和都相等,下图是这个立方体的平面展开图,若20、0、9的对面分别写的是 a、b、c,则a2+b2+c2-ab-bc-ca的值为( )。
A、 B、13 C、 D、15. 一个立方体的每一个面都写有一个自然数,并且相对的两个面内的两数之和都相等,下图是这个立方体的平面展开图,若20、0、9的对面分别写的是 a、b、c,则a2+b2+c2-ab-bc-ca的值为( )。 A、481 B、301 C、602 D、96216. 如图,把一张长方形纸片ABCD沿对角线BD折叠,使C点落在E处,BE与AD相交于点F,下列结论:①BD=AD2+AB2;②△ABF≌△EDF;③ =
A、481 B、301 C、602 D、96216. 如图,把一张长方形纸片ABCD沿对角线BD折叠,使C点落在E处,BE与AD相交于点F,下列结论:①BD=AD2+AB2;②△ABF≌△EDF;③ =④AD=BD•cos45°.其中正确的一组是( )
 A、①② B、②③ C、①④ D、③④17. 若tanA= , 则sinA的值是( )A、 B、 C、3 D、18. 如图所示,河堤横断面迎水坡AB的坡比是1: (坡比是坡面的铅直高度BC与水平宽度AC之比),堤高BC=5m,则坡面AB的长度是( )
A、①② B、②③ C、①④ D、③④17. 若tanA= , 则sinA的值是( )A、 B、 C、3 D、18. 如图所示,河堤横断面迎水坡AB的坡比是1: (坡比是坡面的铅直高度BC与水平宽度AC之比),堤高BC=5m,则坡面AB的长度是( ) A、10m B、10 m C、15m D、5 m19. 如图,PA、PB、CD分别切⊙O于A、B、E,CD交PA、PB于C、D两点,若∠P=40°,则∠PAE+∠PBE的度数为( )
A、10m B、10 m C、15m D、5 m19. 如图,PA、PB、CD分别切⊙O于A、B、E,CD交PA、PB于C、D两点,若∠P=40°,则∠PAE+∠PBE的度数为( ) A、50° B、62° C、66° D、70°20. 如图,⊙O的半径为2,点A的坐标为(2,2 ),直线AB为⊙O的切线,B为切点,则B点的坐标为( )
A、50° B、62° C、66° D、70°20. 如图,⊙O的半径为2,点A的坐标为(2,2 ),直线AB为⊙O的切线,B为切点,则B点的坐标为( )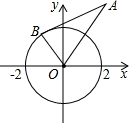 A、(- ) B、(- ,1) C、(- ) D、(-1, )
A、(- ) B、(- ,1) C、(- ) D、(-1, )二、填空题
-
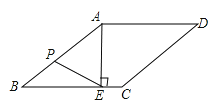
21. 计算:(π﹣3.14)0+2cos60°= .22. 如图,在菱形ABCD中,AE⊥BC,E为垂足,若cosB= , EC=2,P是AB边上的一个动点,则线段PE的长度的最小值是 .
 23. 如图,已知直线l1∥l2∥l3∥l4 , 相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα= .
23. 如图,已知直线l1∥l2∥l3∥l4 , 相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα= . 24. 如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x(x≥0),则x的取值范围是 .
24. 如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x(x≥0),则x的取值范围是 . 25. 如图,平行于x轴的直线AC分别交抛物线 (x≥0)与 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 = .
25. 如图,平行于x轴的直线AC分别交抛物线 (x≥0)与 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 = . 26. 二次函数y=ax2﹣2ax+3的图象与x轴有两个交点,其中一个交点坐标为(﹣1,0),则一元二次方程ax2﹣2ax+3=0的解为27. 在Rt△ABC中,∠C=90°,sinA= ,那么cosA= .28. 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB= ,则AB的长是 .
26. 二次函数y=ax2﹣2ax+3的图象与x轴有两个交点,其中一个交点坐标为(﹣1,0),则一元二次方程ax2﹣2ax+3=0的解为27. 在Rt△ABC中,∠C=90°,sinA= ,那么cosA= .28. 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB= ,则AB的长是 . 29.
29.如图,PA切⊙O于点A,该圆的半径为3,PO=5,则PA的长等于 .
 30.
30.如图,PA、PB是⊙0的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC= .

三、解答题
-
31. 计算:(1)、 -|cos 60°-1|+( )-1-(2017-π)0;(2)、2-1+ -4sin 60°- 0 .32. 如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交于CD、AC于G、E,若EF=32,GE=8,求BE.
 33. 抛物线y=x2+bx+c过点(2,-2)和(-1,10),与x轴交于A、B两点,与y轴交于C点.(1)、求抛物线的解析式.(2)、求△ABC的面积.34. 如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
33. 抛物线y=x2+bx+c过点(2,-2)和(-1,10),与x轴交于A、B两点,与y轴交于C点.(1)、求抛物线的解析式.(2)、求△ABC的面积.34. 如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.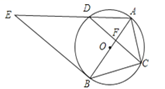 (1)、若CD=2 , AF=3,求⊙O的周长;(2)、求证:直线BE是⊙O的切线.35. 如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
(1)、若CD=2 , AF=3,求⊙O的周长;(2)、求证:直线BE是⊙O的切线.35. 如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度. 36. 36 .如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC, AB相交于点D , E ,连结AD .已知∠CAD=∠B .
36. 36 .如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC, AB相交于点D , E ,连结AD .已知∠CAD=∠B . (1)、求证:AD是⊙O的切线.(2)、若BC=8,tanB= ,求⊙O的半径.37. 如图,O为平面直角坐标系的原点,半径为1的⊙B经过点O,且与x、y轴分别交于A、C两点,点A的坐标为(- ,0),AC的延长线与⊙B的切线OD交于点D,A、B、C三点在同一条直线上.
(1)、求证:AD是⊙O的切线.(2)、若BC=8,tanB= ,求⊙O的半径.37. 如图,O为平面直角坐标系的原点,半径为1的⊙B经过点O,且与x、y轴分别交于A、C两点,点A的坐标为(- ,0),AC的延长线与⊙B的切线OD交于点D,A、B、C三点在同一条直线上. (1)、求OC的长和∠CAO的度数;(2)、求过点D的反比例函数的表达式.38. 已知直线l:y=kx和抛物线C:y=ax2+bx+1.
(1)、求OC的长和∠CAO的度数;(2)、求过点D的反比例函数的表达式.38. 已知直线l:y=kx和抛物线C:y=ax2+bx+1.(Ⅰ)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值;
(Ⅱ)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点;
(i)求此抛物线的解析式;
(ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,求证:OP=PQ.
39. 如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,直线y=﹣ x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
 (1)、求抛物线的解析式;(2)、若PE=5EF,求m的值;(3)、若点E′是点E关于直线PC的对称点、是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若PE=5EF,求m的值;(3)、若点E′是点E关于直线PC的对称点、是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.