浙教版备考2020年中考数学一轮专题12 几何综合复习(2）

试卷更新日期：2020-02-27 类型：一轮复习

进入出卷网下载

一、选择题

1. 如图，一个函数的图象由射线BA，线段BC，射线CD，其中点A（-1，2），B（1，3），C（2，1），D（6，5），则此函数（）

A、当x＜1，y随x的增大而增大 B、当x＜1，y随x的增大而减 C、当x＞1，y随x的增大而增大 D、当x＞1，y随x的增大而减小

查看试题解析
2. 若线段AM，AN分别是△ABC边上的高线和中线，则（）

A、 $A M > A N$ B、 $A M \geq A N$ C、 $A M < A N$ D、 $A M \leq A N$

查看试题解析
3. 欧几里得的《原本》记载，形如x²＋ax=b²的方程的图解法是；画Rt△ABC，使∠ACB=90°，BC= $\frac{a}{2}$ ，AC=b，再在斜边AB上截取BD= $\frac{a}{2}$ 。则该方程的一个正根是（）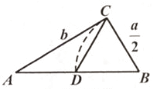

A、AC的长 B、AD的长 C、BC的长 D、CD的长

查看试题解析
4. 如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD=8cm，AE=2cm，则OF的长度是（）

A、3cm B、 $\sqrt{6}$ cm C、2.5cm D、 $\sqrt{5}$ cm

查看试题解析
5. 如图，点C在反比例函数 $y = \frac{k}{x}$ （x＞0）的图象上，过点C的直线与x轴，y轴分别交于点A，B，且AB=BC，△AOB的面积为1，则k的值为（）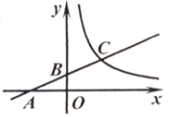

A、1 B、2 C、3 D、4

查看试题解析
6. 在平面直角坐标系xOy中，已知点M，N的坐标分别为（﹣1，2），（2，1），若抛物线y=ax²﹣x+2（a≠0）与线段MN有两个不同的交点，则a的取值范围是（）

A、a≤﹣1或 $\frac{1}{4}$ ≤a＜ $\frac{1}{3}$ B、 $\frac{1}{4}$ ≤a＜ $\frac{1}{3}$ C、a≤ $\frac{1}{4}$ 或a＞ $\frac{1}{3}$ D、a≤﹣1或a≥ $\frac{1}{4}$

查看试题解析
7. 如图，等边三角形ABC边长是定值，点O是它的外心，过点O任意作一条直线分别交AB，BC于点D，E．将△BDE沿直线DE折叠，得到△B′DE，若B′D，B′E分别交AC于点F，G，连接OF，OG，则下列判断错误的是（）

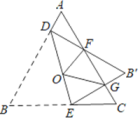A、△ADF≌△CGE B、△B′FG的周长是一个定值 C、四边形FOEC的面积是一个定值 D、四边形OGB'F的面积是一个定值

查看试题解析

二、填空题

8. 如图，公园内有一个半径为20米的圆形草坪，A，B是圆上的点，O为圆心，∠AOB=120°，从A到B只有路弧AB，一部分市民走“捷径”，踩坏了花草，走出了一条小路AB。通过计算可知，这些市民其实仅仅少走了步（假设1步为0.5米，结果保留整数）。（参考数据： $\sqrt{3}$ ≈1.732，π取3.142）

查看试题解析
9. 如图，点A，B是反比例函数y= $\frac{k}{x}$ （x＞0）图象上的两点，过点A，B分别作AC⊥x轴于点C，BD⊥x轴于点D，连接OA，BC，已知点C（2，0），BD=2，S_△BCD=3，则S_△AOC= ．

查看试题解析
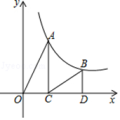10. 如图，AB是⊙的直径，点C是半径OA的中点，过点C作DE⊥AB，交O于点D，E两点，过点D作直径DF，连结AF，则∠DEA=。

查看试题解析
11. 如图，在平面直角坐标系xOy中，已知抛物线y=ax²+bx（a＞0）的顶点为C，与x轴的正半轴交于点A，它的对称轴与抛物线y=ax²（a＞0）交于点B．若四边形ABOC是正方形，则b的值是．

查看试题解析
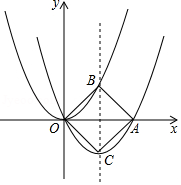12. 等腰三角形ABC中，顶角A为40°，点P在以A为圆心，BC长为半径的圆上，且BP=BA，则∠PBC的度数为。

查看试题解析

三、解答题

13. 如图，在△ABC中，∠ACB=90°，以点B为圆心，BC的长为半径画弧，交线段AB于点D，以点A为圆心，AD长为半径画弧，交线段AC于点E，连结CD。

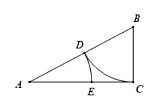(1)、若∠A=28°，求∠ACD的度数；

(2)、设BC=a，AC=b；①线段AD的长度是方程 $x^{2} + 2 a x - b^{2} = 0$ 的一个根吗？说明理由。②若线段AD=EC，求 $\frac{a}{b}$ 的值．

查看试题解析
14. 设二次函数 $y = a x^{2} + b x - (a + b)$ （a，b是常数，a≠0）

(1)、判断该二次函数图象与x轴交点的个数，说明理由．

(2)、若该二次函数的图象经过A（-1，4），B（0，-1），C（1，1）三个点中的其中两个点，求该二次函数的表达式；

(3)、若a+b<0，点P（2，m）（m>0）在该二次函数图象上，求证：a＞0．

查看试题解析
15. 如图，在正方形ABCD中，点G在边BC上（不与点B，C重合），连接AG，作DE⊥AG，于点E，BF⊥AG于点F，设 $\frac{B G}{B C} = k$ 。

(1)、求证：AE=BF；

(2)、连接BE，DF，设∠EDF= $α$ ，∠EBF= $β$ 求证： $k \tan α = k \tan β$

(3)、设线段AG与对角线BD交于点H，△AHD和四边形CDHG的面积分别为S₁和S₂ ，求 $\frac{S_{2}}{S_{1}}$ 的最大值．

查看试题解析
16. 小敏思考解决如下问题：原题：如图1，点P，Q分别在菱形ABCD的边BC，CD上，∠PAQ=∠B，求证AP=AQ。

(1)、小敏进行探索，若将点P，Q的位置特殊化：把∠PAQ绕点A旋转得到∠EAF，使AE⊥BC，点E，F分别在边BC，CD上，如图2，此时她证明了AE=AF。请你证明。

(2)、受以上（1）的启发，在原题中，添加辅助线：如图3，作AE⊥BC，AF⊥CD，垂足分别为E，F。请你继续完成原题的证明。

(3)、如果在原题中添加条件：AB=4，∠B=60°，如图1，请你编制一个计算题（不标注新的字母），并直接给出答案。

查看试题解析
17. 如图，已知AB为⊙O直径，AC是⊙O的切线，连接BC交⊙O于点F，取 $\overset{⌢}{B F}$ 的中点D，连接AD交BC于点E，过点E作EH⊥AB于H．

(1)、求证：△HBE∽△ABC；

(2)、若CF=4，BF=5，求AC和EH的长．

查看试题解析
18. 已知，点M为二次函数y=-（x-b）²＋4b＋1图象的顶点，直线y=mx＋5分别交x轴正半轴，y轴于点A，B。

(1)、判断顶点M是否在直线y=4x＋1上，并说明理由。

(2)、如图1，若二次函数图象也经过点A，B，且mx＋5＞-（x-b）²＋4b＋1，根据图象，写出x的取值范围。

(3)、如图2，点A坐标为（5，0），点M在△AOB内，若点C（ $\frac{1}{4}$ ，y₁），D（ 4，y₂）都在二次函数图象上，试比较y₁与y₂的大小。

查看试题解析
19. 已知，△ABC中，∠B=∠C，P是BC边上一点，作∠CPE=∠BPF，分别交边AC，AB于点E，F。

(1)、若∠CPE=∠C（如图1），求证：PE＋PF=AB。

(2)、若∠CPE≠∠C，过点B作∠CBD=∠CPE，交CA（或CA的延长线）于点D．试猜想：线段PE，PF和BD之间的数量关系，并就∠CPE＞∠C情形（如图2）说明理由。

(3)、若点F与A重合（如图3），∠C=27°，且PA=AE。
①求∠CPE的度数；

②设PB=a，PA=b，AB=c，试证明： $b = \frac{a^{2} - c^{2}}{c}$

查看试题解析
20. 如图，Rt△OAB的直角边OA在x轴上，顶点B的坐标为（6，8），直线CD交AB于点D（6，3），交x轴于点C（12，0）．

(1)、求直线CD的函数表达式；

(2)、动点P在x轴上从点（﹣10，0）出发，以每秒1个单位的速度向x轴正方向运动，过点P作直线l垂直于x轴，设运动时间为t．
①点P在运动过程中，是否存在某个位置，使得∠PDA=∠B？若存在，请求出点P的坐标；若不存在，请说明理由；

②请探索当t为何值时，在直线l上存在点M，在直线CD上存在点Q，使得以OB为一边，O，B，M，Q为顶点的四边形为菱形，并求出此时t的值．

查看试题解析