浙教版备考2020年中考数学一轮专题11 几何综合复习(1）

试卷更新日期：2020-02-27 类型：一轮复习

进入出卷网下载

一、选择题

1. 欧几里得的《原本》记载，形如x²＋ax＝b²的方程的图，解法是：画Rt△ABC，使∠ACB＝90°，BC＝ $\frac{a}{2}$ ，AC＝b，再在斜边AB上截取BD＝ $\frac{a}{2}$ .则该方程的一个正根是（）

A、AC的长 B、AD的长 C、BC的长 D、CD的长

查看试题解析
2. 在Rt△ACB中，∠C＝90°，AC＝BC，一直角三角板的直角顶角O在AB边的中点上，这块三角板绕O点旋转，两条直角边始终与AC，BC边分别相交于E，F，连结EF，则在运动过程中，△OEF与△ABC的关系是（）

A、一定相似 B、当E是AC中点时相似 C、不一定相似 D、无法判断

查看试题解析

二、填空题

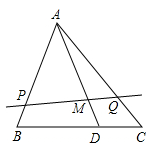
3. 如图所示，在△ABC中，已知BD＝2DC，AM＝3MD，过M作直线交AB，AC于P，Q两点．则 $\frac{A B}{A P} + \frac{2 A C}{A Q}$ ＝．

查看试题解析
4. 如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，分别以AB，AC，BC
为边在AB同侧作正方形ABEF，ACPQ，BDMC，记四块阴影部分的面积分别为S₁ ， S₂ ， S₃ ， S₄ ，则S₁＋S₂＋S₃＋S₄＝．

查看试题解析
5. 过双曲线 $y = \frac{k}{x} (k > 0)$ 上的动点A作AB⊥x轴于点B，P是直线AB上的点，且满足AP=2AB，过点P作x轴的平行线交此双曲线于点C，如果△APC的面积为8，则k的值是。

查看试题解析
6. 在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点．以顶点都是格点的正方形ABCD的边为斜边，向内作四个全等的直角三角形，使四个直角顶点E，F，G，H都是格点，且四边形EFGH为正方形，我们把这样的图形称为格点弦图．例如，在如图1所示的格点弦图中，正方形ABCD的边长为 $\sqrt{13}$ ，此时正方形EFGH的面积为5．问：当格点弦图中的正方形ABCD的边长为 $\sqrt{13}$ 时，正方形EFGH的面积的所有可能值是（不包括5）．

查看试题解析
7. 如图，在矩形ABCD中，AB=4，AD=2，点E在CD上，DE=1，点F是边AB上一动点，以EF为斜边作Rt△EFP．若点P在矩形ABCD的边上，且这样的直角三角形恰好有两个，则AF的值是。

查看试题解析
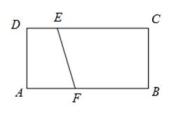8. 如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作 $⊙ P .$ 当 $⊙ P$ 与正方形ABCD的边相切时，BP的长为．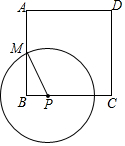

查看试题解析

三、解答题

9. 某兴趣小组在学习了勾股定理之后提出：“锐(钝)角三角形有没有类似于勾股定理的结论”的问题．首先定义了一个新的概念：如图1△ABC中，M是BC的中点，P是射线MA上的点，设 $\frac{A P}{P M}$ ＝k，若∠BPC＝90°，则称k为勾股比．

(1)、如图1，过B，C分别作中线AM的垂线，垂足为E，D.求证：CD＝BE.

(2)、①如图2，当k＝1，且AB＝AC时，AB²＋AC²＝BC²(填一个恰当的数)．
②如图1，当k＝1，△ABC为锐角三角形，且AB≠AC时，①中的结论还成立吗？若成立，请写出证明过程；若不成立，也请说明理由；
③对任意锐角或钝角三角形，如图1，3，请用含勾股比k的表达式直接表示AB²＋AC²与BC²的关系(写出锐角或钝角三角形中的一个即可)．

查看试题解析
10. 如图，△ABC是⊙O的内接三角形，点D在 $\overset{⌢}{B C}$ 上，点E在弦AB上（E不与A重合），且四边形BDCE为菱形．

(1)、求证：AC=CE；

(2)、求证：BC²﹣AC²=AB•AC；

(3)、已知⊙O的半径为3．
①若 $\frac{A B}{A C}$ = $\frac{5}{3}$ ，求BC的长；

②当 $\frac{A B}{A C}$ 为何值时，AB•AC的值最大？

查看试题解析
11. 已知在Rt△ABC中，∠BAC=90°，AB≥AC，D，E分别为AC，BC边上的点（不包括端点），且 $\frac{D C}{B E}$ = $\frac{A C}{B C}$ =m，连结AE，过点D作DM⊥AE，垂足为点M，延长DM交AB于点F．

(1)、如图1，过点E作EH⊥AB于点H，连结DH．
①求证：四边形DHEC是平行四边形；

②若m= $\frac{\sqrt{2}}{2}$ ，求证：AE=DF；

(2)、如图2，若m= $\frac{3}{5}$ ，求 $\frac{D F}{A E}$ 的值．

查看试题解析
12. 如图1，在平面直角坐标系xOy中，已知△ABC，∠ABC=90°，顶点A在第一象限，B，C在x轴的正半轴上（C在B的右侧），BC=2，AB=2 $\sqrt{3}$ ，△ADC与△ABC关于AC所在的直线对称．

(1)、当OB=2时，求点D的坐标；

(2)、若点A和点D在同一个反比例函数的图象上，求OB的长；

(3)、如图2，将第（2）题中的四边形ABCD向右平移，记平移后的四边形为A₁B₁C₁D₁ ，过点D₁的反比例函数y= $\frac{k}{x}$ （k≠0）的图象与BA的延长线交于点P．问：在平移过程中，是否存在这样的k，使得以点P，A₁ ， D为顶点的三角形是直角三角形？若存在，请直接写出所有符合题意的k的值；若不存在，请说明理由．

查看试题解析
13. 如图1，直线l： $y = - \frac{3}{4} x + b$ 与x轴交于点 $A (4 ， 0)$ ，与y轴交于点B，点C是线段OA上一动点 $(0 < AC < \frac{16}{5}) .$ 以点A为圆心，AC长为半径作 $⊙ A$ 交x轴于另一点D，交线段AB于点E，连结OE并延长交 $⊙ A$ 于点F．

(1)、求直线l的函数表达式和 $tan ∠ BAO$ 的值；

(2)、如图2，连结CE，当 $CE = EF$ 时，
$①$ 求证： $△ OCE$ ∽ $△ OEA$ ；

$②$ 求点E的坐标；

(3)、当点C在线段OA上运动时，求 $OE \cdot EF$ 的最大值．

查看试题解析