浙教版备考2020年中考数学一轮专题10 圆 (2)
试卷更新日期:2020-02-27 类型:一轮复习
一、选择题
-
1. 欧几里得的《原本》记载,形如x2+ax=b2的方程的图,解法是:画Rt△ABC,使∠ACB=90°,BC= ,AC=b,再在斜边AB上截取BD= .则该方程的一个正根是( )
 A、AC的长 B、AD的长 C、BC的长 D、CD的长2. 在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC,BC边分别相交于E,F,连结EF,则在运动过程中,△OEF与△ABC的关系是( )
A、AC的长 B、AD的长 C、BC的长 D、CD的长2. 在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC,BC边分别相交于E,F,连结EF,则在运动过程中,△OEF与△ABC的关系是( ) A、一定相似 B、当E是AC中点时相似 C、不一定相似 D、无法判断3. 如图,已知圆内接正三角形的面积为 ,则该圆的内接正六边形的边心距为( )
A、一定相似 B、当E是AC中点时相似 C、不一定相似 D、无法判断3. 如图,已知圆内接正三角形的面积为 ,则该圆的内接正六边形的边心距为( ) A、2 B、1 C、 D、4. 在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线
A、2 B、1 C、 D、4. 在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx-3k+4与⊙O交于B,C两点,则弦BC的长的最小值为.
 5. 已知△ABC的三边a,b,c满足a+b2+|c-6|+28=4 +10b,则△ABC的外接圆半径=.6. 如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 时,阴影部分的面积为
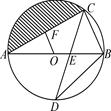
5. 已知△ABC的三边a,b,c满足a+b2+|c-6|+28=4 +10b,则△ABC的外接圆半径=.6. 如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 时,阴影部分的面积为 7. 如图,点P是四边形ABCD外接圆⊙O上任意一点,且不与四边形顶点重合,AD是⊙O的直径,AB=BC=CD,连结PA,PB,PC.若PA=a,则点A到PB和PC的距离之和AE+AF=.
7. 如图,点P是四边形ABCD外接圆⊙O上任意一点,且不与四边形顶点重合,AD是⊙O的直径,AB=BC=CD,连结PA,PB,PC.若PA=a,则点A到PB和PC的距离之和AE+AF=. 8. 如图所示,在△ABC中,已知BD=2DC,AM=3MD,过M作直线交AB,AC于P,Q两点.则 = .
8. 如图所示,在△ABC中,已知BD=2DC,AM=3MD,过M作直线交AB,AC于P,Q两点.则 = .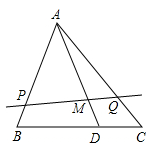 9. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,分别以AB,AC,BC
9. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,分别以AB,AC,BC为边在AB同侧作正方形ABEF,ACPQ,BDMC,记四块阴影部分的面积分别为S1 , S2 , S3 , S4 , 则S1+S2+S3+S4= .

二、解答题