浙教版备考2020年中考数学一轮专题7 三角形

试卷更新日期：2020-02-27 类型：一轮复习

进入出卷网下载

一、选择题

1. 式子2cos30°－tan45°－ $\sqrt{{(1 - \tan 60^{\circ})}^{2}}$ 的值是（）

A、2 $\sqrt{3}$ －2 B、0 C、2 $\sqrt{3}$ D、2

查看试题解析
2. 如图，AB是圆锥的母线，BC为底面直径，已知BC＝6 cm，圆锥的侧面积为15π cm² ，则sin∠ABC的值为（）

A、 $\frac{3}{4}$ B、 $\frac{3}{5}$ C、 $\frac{4}{5}$ D、 $\frac{5}{3}$

查看试题解析
3. 如图，由四个全等的直角三角形围成的大正方形的面积是169，小正方形的面积为49，则sin α－cos α＝（）

A、 $\frac{5}{13}$ B、－ $\frac{5}{13}$ C、 $\frac{7}{13}$ D、－ $\frac{7}{13}$

查看试题解析
4. 如图，在Rt△ABC中，∠ABC＝90°，tan ∠BAC＝2，A(0，a)，B(b，0)，点C在第二象限，BC与y轴交于点D(0，c)，若y轴平分∠BAC，则点C的坐标不能表示为（）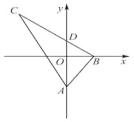

A、(b＋2a，2b) B、(－b－2c，2b) C、(－b－c，－2a－2c) D、(a－c，－2a－2c)

查看试题解析
5. 如图中有四条互相不平行的直线l1，l2，l3，l4所截出的七个角．关于这七个角的度数关系，下列正确的是（）

A、∠2＝∠4＋∠7 B、∠3＝∠1＋∠6 C、∠1＋∠4＋∠6＝180° D、∠2＋∠3＋∠5＝360°

查看试题解析
6. 如图，已知点P是∠AOB的平分线上的一点，∠AOB＝60°，PD⊥OA，M是OP的中点，DM＝4 cm.如果点C是OB上一个动点，则PC的最小值为（）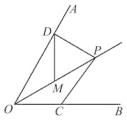

A、2 cm B、2 $\sqrt{3}$ cm C、4 cm D、4 $\sqrt{3}$ cm

查看试题解析
7. 如图，在△ABC中，AB＝AC＝5，BC＝8，点P是BC边上的动点，过点P作PD⊥AB于点D，PE⊥AC于点E，则PD＋PE的长是（）

A、4.8 B、4.8或3.8 C、3.8 D、5

查看试题解析
8. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC 交AB于点E，交AC于点F，过点O作OD⊥AC于点D，下列四个结论：①EF＝BE＋CF； ②∠BOC＝90°＋ $\frac{1}{2}$ ∠A；③点O到△ABC各边的距离相等；④设OD＝m，AE＋AF＝n，则S_△AEF＝mn.

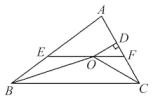
其中正确的结论是（）

A、①②③ B、①②④ C、②③④ D、①③④

查看试题解析

二、填空题

9. 计算：sin² 60°＋cos 60°－tan 45°＝

查看试题解析
10. 若△ABC的两边长分别为2和3，第三边的长是方程x²－8x＋15＝0的根，则△ABC的周长是.

查看试题解析
11. 如图，OC为∠AOB的平分线，CM⊥OB，OC＝5，OM＝4，则点C到射线OA的距离为．

查看试题解析
12. 如图，在四边形ABCD中，AB＝ $\sqrt{29}$ ，AD＝7，BC＝8，tan ∠B＝ $\frac{5}{2}$ ，∠C＝∠D，则线段CD的长为．

查看试题解析

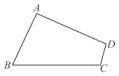
三、解答题

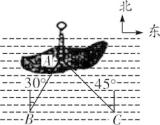
13. 如图，湖中的小岛上有一标志性建筑物，其底部为A，某人在岸边的B处测得A在B的北偏东30°的方向上，然后沿岸边直行4公里到达C处，再测得A在C的北偏西45°的方向上(其中A，B，C在同一平面上)．求这个标志性建筑物底部A到岸边BC的最短距离．

查看试题解析
14. 已知：在△ABC中，AB＝AC，D为AC的中点，DE⊥AB，DF⊥BC，垂足分别为点E，F，且DE＝DF.求证：△ABC是等边三角形．

查看试题解析
15. 在△ABM中，∠ABM＝45°，AM⊥BM，垂足为M.点C是BM延长线上一点，连结AC.

(1)、如图1，若AB＝3 $\sqrt{2}$ ，BC＝5，求AC的长．

(2)、如图2，点D是线段AM上一点，MD＝MC，点E是△ABC外一点，
EC＝AC，连结ED并延长交BC于点F，且点F是线段BC的中点，求证：∠BDF＝∠CEF.

查看试题解析
16. 如图，在四边形ABCD中，∠DAB＝90°，DB＝DC，点E，F分别为DB，BC的中点，连结AE，EF，AF.

(1)、求证：AE＝EF；

(2)、当AF＝AE时，设∠ADB＝α，∠CDB＝β，求α，β之间的数量关系．

查看试题解析