浙教版备考2020年中考数学一轮专题5 概率统计
试卷更新日期：2020-02-27 类型：一轮复习
一、选择题
-
1. “若a是实数，则|a|≥0”这一事件是（ ）A、必然事件 B、不确定事件 C、不可能事件 D、随机事件2. 下列说法正确的是（ ）A、为了解我国中学生课外阅读的情况，应采用全面调查的方式 B、一组数据1，2，5，5，5，3，3的中位数和众数都是5 C、抛掷一枚硬币100次，一定有50次“正面朝上” D、甲组数据的方差是0.03，乙组数据的方差是0.1，则甲组数据比乙组数据稳定3. 某学校将为七年级学生开设A，B，C，D，E，F共6门选修课，现选取若干学生进行了“我最喜欢的一门选修课”调查，将调查结果绘制成如图统计图表(不完整)
选修课
A
B
C
D
E
F
人数
40
60
100
根据图表提供的信息，下列结论错误的是( )
A、这次被调查的学生人数为400人 B、扇形统计图中E部分扇形的圆心角为72° C、被调查的学生中喜欢选修课E，F的人数分别为80，70 D、喜欢选修课C的人数最少4. 测试五位学生的“一分钟跳绳”的成绩，得到五个各不相同的数据，在统计时，出现了一处错误：将最高成绩写得更高了，计算结果不受影响的是（ ）A、方差 B、标准差 C、中位数 D、平均数5. 如图，在平面直角坐标系中，点A1 ， A2在x轴上，点B1 ， B2在y轴上，其坐标分别为A1(1，0)，A2(2，0)，B1(0，1)，B2(0，2)，分别以A1 ， A2 ， B1 ， B2其中的任意两点与点O为顶点作三角形，所作三角形是等腰三角形的概率是（ ）
A、 B、 C、 D、6. 如图，将一块菱形ABCD硬纸片固定后进行投针训练．已知纸片上AE⊥BC于E，CF⊥AD于F，sinD= ．若随意投出一针命中了菱形纸片，则命中矩形区域的概率是（ ）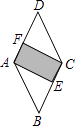
A、 B、 C、 D、二、填空题
-
7. 在一个不透明的盒子中装有n个球,它们除了颜色之外其他都没有区别,其中含有3个红球,每次摸球前,将盒中所有的球摇匀,然后随机摸出一个球,记下颜色后再放回盒中.通过大量重复试验,发现摸到红球的频率稳定在0.03,那么可以推算出n的值大约是 .8. 一组数据2，x，1，3，5，4，若这组数据的中位数是3，则这组数据的方差是 ．
9. 两组数据m，6，n与1，m，2n，7的平均数都是6，若将这两组数据合并成一组数据，则这组新数据的中位数为 ．
10. 如图，四边形ABCD中，AD∥BC，AB＝DC，∠ABC＝60°.若其四边满足：长度的众数为5，平均数为 ，上、下底之比为1∶2，则BD＝ ．
11. 有9张卡片,分别写有1~9这九个数字(卡片上的数字互不相同),将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,则使关于x的不等式组 有解的概率为 .三、解答题
-
12. 在第23个世界读书日前夕我市某中学为了解本校学生的每周课外阅读时间(用t表示，单位：小时)，采用随机抽样的方法进行问卷调查，调查结果按0≤t<2，2≤t<3，3≤t<4，t≥4分为四个等级，并依次用A，B，C，D表示.根据调查结果统计的数据绘制成了如图K32-5所示的两幅不完整的统计图，由图中给出的信息解答下列问题：
(1)、求本次调查的学生人数；(2)、求扇形统计图中等级B所在扇形的圆心角度数，并把条形统计图补充完整；(3)、若该校共有学生1200人，试估计每周课外阅读时间满足3≤t<4的人数.13. 某运动品牌对第一季度A，B两款运动鞋的销售情况进行统计，两款运动鞋的销售量及总销售额如图所示：
(1)、一月份B款运动鞋的销售量是A款的 ，求一月份B款运动鞋销售了多少双？(2)、第一季度这两款运动鞋的销售单价保持不变，求三月份的总销售额(销售额＝销售单价×销售量)．(3)、结合第一季度的销售情况，请你对这两款运动鞋的进货、销售等方面提出一条建议．14. 有有三张正面分别写有数字－2，－1，1的卡片，它们的背面完全相同，将这三张卡片背面朝上洗匀后随机抽取一张，以其正面的数字作为x的值，放回卡片洗匀，再从三张卡片中随机抽取一张，以其正面的数字作为y的值，两次结果记为(x，y)．(1)、用树状图或列表法表示(x，y)所有可能出现的结果；(2)、求使分式 ＋ 有意义的(x，y)出现的概率；(3)、化简分式 ＋ ，并求使分式的值为整数的(x，y)出现的概率．