浙教版备考2020年中考数学一轮专题1 数与式

试卷更新日期：2020-02-27 类型：一轮复习

进入出卷网下载

一、选择题

1. 下列说法中错误的有（）个
（ 1 ）一个无理数与一个有理数的和是无理数；（2）一个无理数与一个有理数的积是无理数；（3）两个无理数和是无理数；（4）两个无理数积是无理数．

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 实数a，b，c，d在数轴上的对应点的位置如图所示，则正确的是（）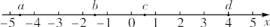

A、a＞－4 B、bd＞0 C、|a|＞|d| D、b＋c＞0

查看试题解析
3. 若多项式x⁵－(m－2)x^my＋4y⁵是五次三项式，则正整数m可以取（）

A、4 B、1，3，4 C、1，2，3，4 D、2，3，4

查看试题解析
4. G20峰会来了，在全民的公益热潮中，杭州的志愿者们摩拳擦掌，想为世界展示一个美丽幸福文明的杭州．据统计，目前杭州市注册志愿者已达9.17×10⁵人．而这个数字，还在不断地增加．请问近似数9.17×10⁵的精确度是（　　）

A、百分位 B、个位 C、千位 D、十万位

查看试题解析
5. 把8a³-8a²+2a进行因式分解，结果正确的是（）

A、2a(4a²-4a+1) B、8a²(a-1) C、2a(2a-1)² D、2a(2a+1)²

查看试题解析
6. 已知y＝ $\sqrt{2 x - 5}$ ＋ $\sqrt{5 - 2 x}$ －3，则2xy的值为（）

A、－15 B、15 C、－ $\frac{15}{2}$ D、 $\frac{15}{2}$

查看试题解析
7. 下列分式中，最简分式是（）

A、 $\frac{3 x^{2}}{4 x y}$ B、 $\frac{x^{2} + y^{2}}{x + y}$ C、 $\frac{x - 2}{x^{2} - 4}$ D、 $\frac{1 + x}{x^{2} + 2 x + 1}$

查看试题解析
8. 若 $\sqrt{3}$ <a< $\sqrt{10}$ ，则下列结论中正确的是（）

A、1<a<3 B、1<a<4 C、2<a<3 D、2<a<4

查看试题解析
9. 若x²+mx-15=(x+3)(x+n)，则m的值为( )

A、-5 B、5 C、-2 D、2

查看试题解析
10. 已知a是方程x²＋x－1＝0的一个根，则 $\frac{2}{a^{2} - 1} - \frac{1}{a^{2} - a}$ 的值为（）

A、 $\frac{- 1 + \sqrt{5}}{2}$ B、 $\frac{- 1 \pm \sqrt{5}}{2}$ C、－1 D、1

查看试题解析
11. 已知a，b，c是△ABC的三边长，且满足a³＋ab²＋bc²＝b³＋a²b＋ac² ，则△ABC的形状是（）

A、等腰三角形 B、直角三角形 C、等腰三角形或直角三角形 D、等腰直角三角形

查看试题解析
12. 请你计算：(1-x)(1+x)，(1-x)(1+x+x²)，…，则(1-x)(1+x+x²+…+xⁿ)的结果是（）

A、1-xⁿ⁺¹ B、1+xⁿ⁺¹ C、1-xⁿ D、1+xⁿ

查看试题解析
13. 一个三角形的三边长分别为1，k，4，化简|2k－5|－ $\sqrt{k^{2} - 12 k + 36}$ 的结果是（）

A、3k－11 B、k＋1 C、1 D、11－3k

查看试题解析
14. 在矩形ABCD内将两张边长分别为a和b(a>b)的正方形纸片
按图K2-4①②两种方式放置(图K2-4①②中两张正方形纸片均有部分重叠)，矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图①中阴影部分的面积为S₁ ，图②中阴影部分的面积为S₂.当AD-AB=2时， S₂-S₁的值为（）

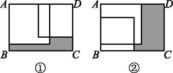A、2a B、2b C、2a-2b D、-2b

查看试题解析

二、填空题

15. 如果 $\sqrt{2 a + b^{2}}$ ＋|b²－10|＝0，则a＋b的值为

查看试题解析
16. 已知代数式x²-mx+9是完全平方式，则常数m=.

查看试题解析
17. 化简(π－3.14)⁰＋|1－2 $\sqrt{2}$ |－ $\sqrt{8}$ ＋( $\frac{1}{2}$ )^－1的结果是

查看试题解析
18. 若m＋ $\frac{1}{m}$ ＝3，则m²＋ $\frac{1}{m^{2}}$ ＝

查看试题解析
19. 等式 $\frac{\sqrt{x -3}}{\sqrt{x + 1}}$ = $\sqrt{\frac{x -3}{x + 1}}$ 成立的x的条件是．

查看试题解析
20. 如果 $\sqrt[3]{68.8}$ ＝4.098， $\sqrt[3]{a}$ ＝40.98，那么a＝
$\sqrt{2017} \approx 44.91$ ， $\sqrt{201.7} \approx 14.0$ ，则 $\sqrt{20.17} \approx$

查看试题解析
21. 若x满足|2017-x|+ $\sqrt{x -2018}$ =x，则x-2017²=

查看试题解析
22. 有理数a、b、c在数轴上的点如图，则 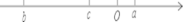$| c | + | a - c | - 2 | c + b | + | a + b |$ =

查看试题解析

三、解答题

23. 计算

(1)、(－ $\frac{1}{2}$ )²－ $\frac{1}{2^{2}}$ ＋(－1)^{2 017}－1 $\frac{1}{2}$ ×(0.5－ $\frac{2}{3}$ )÷1 $\frac{1}{9}$ .

(2)、|－3|＋(π－2017)⁰－2sin30°＋( $\frac{1}{3}$ )^－1

(3)、(2 $\sqrt{5}$ - $\sqrt{2}$ )⁰+|2- $\sqrt{5}$ |+(-1)²⁰¹⁷- $\frac{1}{3}$ × $\sqrt{45}$ ;

查看试题解析
24. 若a，b，c都是非零有理数，求 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |}$ 的值．

查看试题解析
25. 已知a，b为常数，且三个单项式4xy² ， axy^b ，－5xy相加得到的和仍是单项式，求a，b的值．

查看试题解析
26. 先化简，再求值：(a＋b)(a－b)＋(a－b)²－(2a²－ab)，其中a，b是一元二次方程x²＋x－2＝0的两个实数根．

查看试题解析
27. 已知关于x的二次三项式x²+mx+n有一个因式为x+5，且m+n=17，试求m，n的值.

查看试题解析
28. 设 $\frac{x}{x^{2} + x + 1}$ ＝a(a≠0)，求 $\frac{x^{2}}{x^{4} + x^{2} + 1}$ 的值．

查看试题解析
29. 已知A= $\frac{x^{2} + 2 x + 1}{x^{2} -1}$ - $\frac{x}{x -1}$ .

(1)、化简A;

(2)、当x满足不等式组 ${\begin{array}{l} x -1 \geq 0, \\ x -3 < 0 \end{array}$ 且为整数时，求A的值.

查看试题解析

四、应用题

30. 如图，将一张矩形纸板按照图中虚线裁剪成九块，其中有两块是边长都为m的大正方形，两块是边长都为n的小正方形，五块是长为m，宽为n的全等小矩形，且m>n，(以上长度单位：cm)

(1)、观察图形，可以发现代数式2m²＋5mn＋2n²可以因式分解为；

(2)、若每块小矩形的面积为10 cm² ，四个正方形的面积和为58 cm² ，试求图中所有裁剪线(虚线部分)长之和．

查看试题解析

31. 某公司派出甲车前往某地完成任务，此时，有一辆流动加油车与他同时出发，

且在同一条公路上匀速行驶（速度保持不变）．为了确定汽车的位置，我们用OX表示这条公路，原点O为零千米路标，并作如下约定：速度为正，表示汽车向数轴的正方向行驶；速度为负，表示汽车向数轴的负方向行驶；速度为零，表示汽车静止．行程为正，表示汽车位于零千米的右侧；行程为负，表示汽车位于零千米的左侧；行程为零，表示汽车位于零千米处．两车行程记录如表：

时间（h）	0	5	7	x
甲车位置（km）	190	-10
流动加油车位（km）		170	270

由上面表格中的数据，解决下列问题：

(1)、甲车开出7小时时的位置为km，流动加油车出发位置为km；

(2)、当两车同时开出x小时时，甲车位置为km，流动加油车位置为km （用x的代数式表示）；

(3)、甲车出发前由于未加油，汽车启动后司机才发现油箱内汽油仅够行驶3小时，问：甲车连续行驶3小时后，能否立刻获得流动加油车的帮助？请说明理由．

查看试题解析