广西来宾市2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-02-26 类型:期末考试
一、选择题:本大题共12小题,每小题3分,共36分,在每小题给出的四个选项中,只有一项符合题目要求。
-
1. 已知反比例函数y= ,则其图象在平面直角坐标系中可能是( )A、
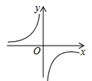 B、
B、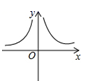 C、
C、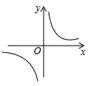 D、
D、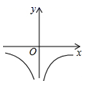 2. 一元二次方程5x2-2x=0的解是( )A、x1=0,x2= B、x1=0,x2= C、x1=0,x2= D、x1=0,x2=3. cos60°-sin30°+tan45°的值为( )A、2 B、-2 C、-1 D、14. 如图,AB∥CD,AC,BD,EF相交于点O,则图中相似三角形共有( )
2. 一元二次方程5x2-2x=0的解是( )A、x1=0,x2= B、x1=0,x2= C、x1=0,x2= D、x1=0,x2=3. cos60°-sin30°+tan45°的值为( )A、2 B、-2 C、-1 D、14. 如图,AB∥CD,AC,BD,EF相交于点O,则图中相似三角形共有( )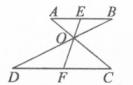 A、1对 B、2对 C、3对 D、4对5. 如图所示,A,B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠BAC=90°,∠ACB=40°,则AB等于( )
A、1对 B、2对 C、3对 D、4对5. 如图所示,A,B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠BAC=90°,∠ACB=40°,则AB等于( )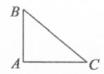 A、asin40°米 B、acos40°米 C、atan40°米 D、 米6. m,n是一元二次方程x2-5x-2=0的两个实数根,则m+n-mn的值是( )A、-7 B、7 C、3 D、-37. 对于反比例函数y= ,下列说法正确的是( )A、点(-2,1)在它的图象上 B、它的图象经过原点 C、它的图象在第一、三象限 D、当x>0时,y随x的增大而增大8. 已知3是关于x的方程x2-5x+c=0的一个根,则这个方程的另一个根是( )A、-2 B、2 C、5 D、69. 堤坝的横断面如图,堤高BC是5米,迎水斜坡AB的长为13米,那么斜坡AB的坡度是( )
A、asin40°米 B、acos40°米 C、atan40°米 D、 米6. m,n是一元二次方程x2-5x-2=0的两个实数根,则m+n-mn的值是( )A、-7 B、7 C、3 D、-37. 对于反比例函数y= ,下列说法正确的是( )A、点(-2,1)在它的图象上 B、它的图象经过原点 C、它的图象在第一、三象限 D、当x>0时,y随x的增大而增大8. 已知3是关于x的方程x2-5x+c=0的一个根,则这个方程的另一个根是( )A、-2 B、2 C、5 D、69. 堤坝的横断面如图,堤高BC是5米,迎水斜坡AB的长为13米,那么斜坡AB的坡度是( )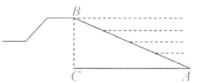 A、1:3 B、1:2.6 C、1:2 D、1:2.410. 某文具店将进价为30元的钢笔,以50元售出,平均每月能售出300支,经试销发现每支钢笔每涨价10元,其月销售量就减少10支,为实现每月利润8000元,设定价为x,则可得方程( )A、300(x-30)=8000 B、300(x-50)=8000 C、(x-30)[300-(x-50)]=8000 D、x-30=800011. 平行四边形ABCD两邻边长分别为2和3,它们的夹角(锐角)为60°,则平行四边形ABCD中较短的对角线的长为( )
A、1:3 B、1:2.6 C、1:2 D、1:2.410. 某文具店将进价为30元的钢笔,以50元售出,平均每月能售出300支,经试销发现每支钢笔每涨价10元,其月销售量就减少10支,为实现每月利润8000元,设定价为x,则可得方程( )A、300(x-30)=8000 B、300(x-50)=8000 C、(x-30)[300-(x-50)]=8000 D、x-30=800011. 平行四边形ABCD两邻边长分别为2和3,它们的夹角(锐角)为60°,则平行四边形ABCD中较短的对角线的长为( ) A、 B、 C、3 D、112. 如图,点A、B分别是反比例函数y= 与正比例函数y=k1x,y=k2x的交点,过点A作x轴的垂线AC,垂足为C,线段AC与直线y=k2x交于点D,若△ADO的面积为4,点D为线段OB的三等分点,则k的值为( )
A、 B、 C、3 D、112. 如图,点A、B分别是反比例函数y= 与正比例函数y=k1x,y=k2x的交点,过点A作x轴的垂线AC,垂足为C,线段AC与直线y=k2x交于点D,若△ADO的面积为4,点D为线段OB的三等分点,则k的值为( )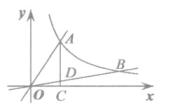 A、 B、4 C、8 D、9
A、 B、4 C、8 D、9二、填空题:本大题共6小题,每小题3分,共18分。
-
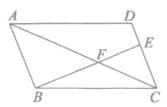
13. 如图,在 ABCD中,点E在DC上,若EC:AB=2:3,则C△ECF:C△BAF=。
 14. 某校开展“节约每一滴水”活动,为了了解开展活动一个月以来节约用水的情况,从八年级的400名同学中选取20名同学统计了各自家庭一个月节约用水情况,如表:
14. 某校开展“节约每一滴水”活动,为了了解开展活动一个月以来节约用水的情况,从八年级的400名同学中选取20名同学统计了各自家庭一个月节约用水情况,如表:节水金港国际/m3
0.2
0.25
0.3
0.4
0.5
家庭数/个
2
4
6
7
1
请你估计这400名同学的家庭一个月节约用水的总量大约是 m3。
15. 在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,若一根电线杆的影长为2米,则电线杆为米。16. 如图,已知点C为反比例函数y= 图象上的一点,过点C向坐标轴引垂线,垂足为A、B,那么四边形AOBC的面积为。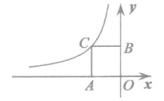 17. 已知锐角A满足4sin2A=3,则∠A=。18. 如图所示,在矩形ABCD中,AB=4,BC= ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF= ,则CE=。
17. 已知锐角A满足4sin2A=3,则∠A=。18. 如图所示,在矩形ABCD中,AB=4,BC= ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF= ,则CE=。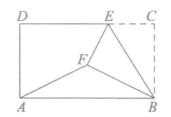
三、解答题:本大题共8小題,共66分,解答应写出文字说明、证明过程或演算步骤.
-
19. 用适当的方法解下列方程(1)、4(x-3)2-25=0(2)、2x2+7x-4=0。20. 如图,已知O是坐标原点,A,B两点的坐标分别为(3,-1),(2,1)
 (1)、以点O为位似中心,在y轴的左侧将△OAB放大2倍;(2)、分别写出A,B两点的对应点A’,B’的坐标。21. 某校为了解1600名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查。问卷给出了五种上学方式供学生选择,每人必选一项,且只能选一项.请根据下面两个不完整的统计图回答以下问题:
(1)、以点O为位似中心,在y轴的左侧将△OAB放大2倍;(2)、分别写出A,B两点的对应点A’,B’的坐标。21. 某校为了解1600名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查。问卷给出了五种上学方式供学生选择,每人必选一项,且只能选一项.请根据下面两个不完整的统计图回答以下问题: (1)、在这次调查中,共抽取了多少名学生;(2)、补全两个统计图;(3)、估计全校所有学生中有多少人乘坐公交车上学。22. 如图,在Rt△ABC中,∠C=90,BC=8,tanB= ,点D在BC上,且BD=AD。求AC的长和cos∠ADC的值。
(1)、在这次调查中,共抽取了多少名学生;(2)、补全两个统计图;(3)、估计全校所有学生中有多少人乘坐公交车上学。22. 如图,在Rt△ABC中,∠C=90,BC=8,tanB= ,点D在BC上,且BD=AD。求AC的长和cos∠ADC的值。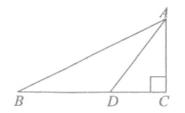 23. 已知关于x的一元二次方程x2-2x-a=0(1)、如果此方程有两个不相等的实数根,求a的取值范围;(2)、如果此方程的两个实数根为x1 , x2 , 且满足 ,求a的值。24. 某地计划对矩形广场进行扩建改造,如图,原广场长50m,宽40m,要求扩建后的矩形广场的长与宽的比为3:2.扩充区域的扩建费用为每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用为每平方米100元.如果计划总费用为642000元,那么扩建后广场的长和宽分别是多少m?
23. 已知关于x的一元二次方程x2-2x-a=0(1)、如果此方程有两个不相等的实数根,求a的取值范围;(2)、如果此方程的两个实数根为x1 , x2 , 且满足 ,求a的值。24. 某地计划对矩形广场进行扩建改造,如图,原广场长50m,宽40m,要求扩建后的矩形广场的长与宽的比为3:2.扩充区域的扩建费用为每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用为每平方米100元.如果计划总费用为642000元,那么扩建后广场的长和宽分别是多少m? 25. 两个全等的等腰直角三角形按如图方式放置在平面直角坐标系中,OA在x轴上,且∠COD=∠OAB=90°,OC= ,反比例函数y= 的图象经过点B。
25. 两个全等的等腰直角三角形按如图方式放置在平面直角坐标系中,OA在x轴上,且∠COD=∠OAB=90°,OC= ,反比例函数y= 的图象经过点B。 (1)、求k的值;(2)、将△OCD沿射线OB移动,当点D落在y= 的图象上时,求点D经过的路径长。26. 回答下列题目
(1)、求k的值;(2)、将△OCD沿射线OB移动,当点D落在y= 的图象上时,求点D经过的路径长。26. 回答下列题目 (1)、如图①,在矩形ABCD中,AB=6,BC=4,E,F分别是BC,AB上的点,且DF⊥AE,求 的值。(2)、如图②,在矩形ABCD中, (k为常数),将矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形EFGH,EH交CD于点P,连接AE交GF于点O,求 的值;(3)、在(2)的条件下,连接CP,当k= 时,若tan∠CGH= ,GF=2 ,求CP的长。
(1)、如图①,在矩形ABCD中,AB=6,BC=4,E,F分别是BC,AB上的点,且DF⊥AE,求 的值。(2)、如图②,在矩形ABCD中, (k为常数),将矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形EFGH,EH交CD于点P,连接AE交GF于点O,求 的值;(3)、在(2)的条件下,连接CP,当k= 时,若tan∠CGH= ,GF=2 ,求CP的长。