辽宁省盘锦市大洼区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-26 类型:期末考试
一、单选题
-
1. 下列长度的三条线段,能组成三角形的是( )A、2cm,3cm,5cm B、8cm,8cm,15cm C、8cm,4cm,4cm D、6cm,7cm,13cm2. 下面四个手机应用图标中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、5a2-2a2=3 B、a2÷a=a2 C、a2•a3=a6 D、(-ab)2=a2b24. 已知一个多边形的内角和是外角和的3倍,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形5. 如图,将两根钢条 AA',BB' 的中点连接在一起,使AA',BB' 可以绕着点O自由转动,就做成了一个测量工具(卡钳),则图中AB的长等于内槽宽 A′B′ ,那么判定 △OAB≌△OA′B′ 的理由是( )
3. 下列运算正确的是( )A、5a2-2a2=3 B、a2÷a=a2 C、a2•a3=a6 D、(-ab)2=a2b24. 已知一个多边形的内角和是外角和的3倍,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形5. 如图,将两根钢条 AA',BB' 的中点连接在一起,使AA',BB' 可以绕着点O自由转动,就做成了一个测量工具(卡钳),则图中AB的长等于内槽宽 A′B′ ,那么判定 △OAB≌△OA′B′ 的理由是( )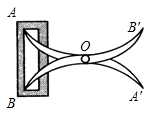 A、边角边 B、边边边 C、角边角 D、角角边6. 如果x2+4x+k2是一个完全平方式,那么常数k的值为( )A、4 B、2 C、-2 D、±27.
A、边角边 B、边边边 C、角边角 D、角角边6. 如果x2+4x+k2是一个完全平方式,那么常数k的值为( )A、4 B、2 C、-2 D、±27.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
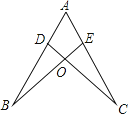 A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD8. 把分式 中的a、b都扩大2倍,则分式的值( )
A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD8. 把分式 中的a、b都扩大2倍,则分式的值( )
A、扩大2倍 B、不变 C、扩大4倍 D、缩小2倍9. 如图,在等边三角形ABC中,BC=2,D是AB的中点,过点D作DF⊥AC于点F,过点F作EF⊥BC于点E,则BE的长为( )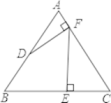 A、1 B、
A、1 B、 C、
C、 D、
D、 10. 如图,等腰三角形ABC的底边BC为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为 ( )
10. 如图,等腰三角形ABC的底边BC为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为 ( )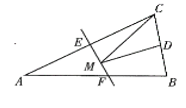 A、8 B、10 C、12 D、14
A、8 B、10 C、12 D、14二、填空题
-
11. 已知等腰三角形一边长为3,另一边长为7,则这个等腰三角形的周长为。12. 某流感病毒的直径大约为0.000 000 08lm,用科学记数法表示为13. 因式分解:2x2﹣8=;(x2+1)2﹣4x2=;x2﹣x﹣12= .14. 分式 有意义,则x的取值范围是。15. 如图,在
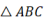 中,
中, 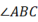 和
和 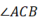 的平分线交于点
的平分线交于点 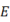 ,过点
,过点 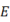 作
作 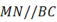 交
交 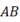 于
于 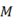 ,交
,交 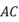 于
于 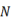 ,若
,若 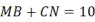 ,那么线段
,那么线段 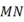 的长为 .
的长为 . 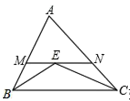 16. 已知a+b=5,ab=4,则2a2+2b2=。17. 如图,△ABC的三边AB、BC、CA长分别为30、40、50.其三条角平分线交于点O,则S△ABO :S△BCO :S△CAO =。
16. 已知a+b=5,ab=4,则2a2+2b2=。17. 如图,△ABC的三边AB、BC、CA长分别为30、40、50.其三条角平分线交于点O,则S△ABO :S△BCO :S△CAO =。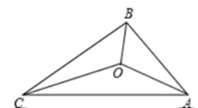 18. 已知△ABC中,AH⊥BC,垂足为H,若AB+BH=CH,∠ABH=80°,则∠BAC= 。
18. 已知△ABC中,AH⊥BC,垂足为H,若AB+BH=CH,∠ABH=80°,则∠BAC= 。三、解答题
-
19. 计算题(1)、(-4x)(2x+y)+(24x3y-12x2y2)÷6xy(2)、(x-8y)(4x-y)-(2x+y)(2x-y)20. 解方程(1)、(2)、
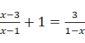 21. 先化简,再求值: , 其中 |x|=2.
21. 先化简,再求值: , 其中 |x|=2.
22. 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-3,2),B(-4,-3),C(-1,-1)。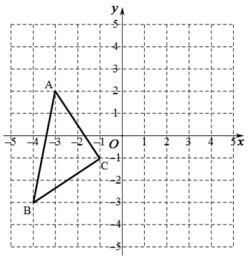 (1)、写出△ABC关于x轴对称的△A1B1C1 的各顶点坐标;(2)、画出△ABC关于y轴对称的△A2B2C2;(3)、求△A2B2C2的面积。23. 如图,在△ ABC中,AB=AC,点D在线段BC上,AD=BD,△ ADC是等腰三角形,求△ABC三个内角的度数。
(1)、写出△ABC关于x轴对称的△A1B1C1 的各顶点坐标;(2)、画出△ABC关于y轴对称的△A2B2C2;(3)、求△A2B2C2的面积。23. 如图,在△ ABC中,AB=AC,点D在线段BC上,AD=BD,△ ADC是等腰三角形,求△ABC三个内角的度数。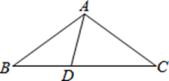 24. 为推进垃圾分类,推动绿色发展,某工厂购进甲、乙两种型号的机器人用来进行垃圾分类,甲型机器人比乙型机器人每小时多分20kg,甲型机器人分类800kg垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等。
24. 为推进垃圾分类,推动绿色发展,某工厂购进甲、乙两种型号的机器人用来进行垃圾分类,甲型机器人比乙型机器人每小时多分20kg,甲型机器人分类800kg垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等。
(1)、两种机器人每小时分别分类多少垃圾?(2)、现在(2)两种机器人共同分类700kg垃圾,工作2小时后甲型机器人因机器维修退出,求甲型机器人退出后乙型机器人还需工作多长时间才能完成?
25. 如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD =∠BCE = 90°,点M为AN的中点,过点E与AD平行的直线交射线AM于点N。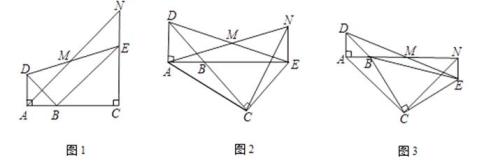 (1)、当A,B,C三点在同一直线上时(如图1),求证:AD=NE ;(2)、将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;(3)、将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,请证明;若不成立,请说明理由。
(1)、当A,B,C三点在同一直线上时(如图1),求证:AD=NE ;(2)、将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;(3)、将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,请证明;若不成立,请说明理由。