辽宁省沈阳市大东区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-26 类型:期末考试
一、单选题
-
1. 以下列各组数为三角形的三边,能构成直角三角形的是( )A、4,5,6 B、1,1, C、6,8,11 D、5,12,232. 下列各数中,是无理数的是( )A、3.1415 B、 C、 D、3. 下列各点中,在第三象限的点是( )A、 B、 C、 D、4. 下列各式中,无论 为任何数都没有意义的是( )A、 B、 C、 D、5. 某班 名同学一周参加体育锻炼时间统计如表所示:
人数(人)
时间(小时)
那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A、 , B、 , C、 , D、 ,6. 已知a,b满足方程组 则a+b的值为( )
A、﹣4 B、4 C、﹣2 D、27. 下列命题中的假命题是( )A、两直线平行,内错角相等 B、同位角相等,两直线平行 C、两直线平行,同旁内角相等 D、平行于同一条直线的两直线平行8. 如图所示是一条街道的路线图,若AB∥CD,且∠ABC=130°,那么当∠CDE等于( )时,BC∥DE. A、40° B、50° C、70° D、130°9. 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )
A、40° B、50° C、70° D、130°9. 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )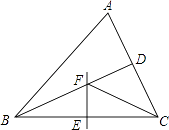 A、48° B、36° C、30° D、24°10. 若函数 的值随自变量的增大而增大,则函敷 的图象大致是( )A、
A、48° B、36° C、30° D、24°10. 若函数 的值随自变量的增大而增大,则函敷 的图象大致是( )A、 B、
B、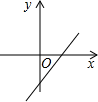 C、
C、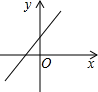 D、
D、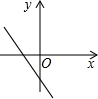
二、填空题
-
11. 16的平方根是 ,9的立方根是 .12. 已知 是关于 , 的二元一次方程,则 .13. 点P(1,-2)关于y轴对称的点P'的坐标为.
14. 如图,数轴上的点 表示的数是 , ,垂足为 ,且 ,以点 为圆心. 为半径画弧交数轴于点 ,则 点表示的数为.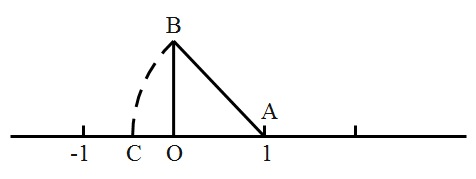 15. 李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是升.
15. 李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是升.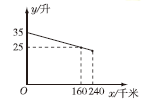 16. 等腰 中, 是BC边上的高,且 ,则等腰 底角的度数为.
16. 等腰 中, 是BC边上的高,且 ,则等腰 底角的度数为.三、解答题
-
17. 计算:(1)、(2)、18. 如图,在 中, , , ,点 是 外一点,连接 , ,且 , .
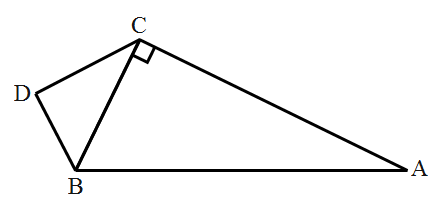 (1)、求 的长:(2)、求证:在 是直角三角形.19. 列二元一次方程组解应用题:学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买 个 奖品和 个 奖品共需 元;购买 个 奖品和 个 奖品共需 元.求 , 两种奖品的单价.20. 甲、乙、丙三位运动员在相同条件下各射靶 次,每次射靶的成绩如下:
(1)、求 的长:(2)、求证:在 是直角三角形.19. 列二元一次方程组解应用题:学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买 个 奖品和 个 奖品共需 元;购买 个 奖品和 个 奖品共需 元.求 , 两种奖品的单价.20. 甲、乙、丙三位运动员在相同条件下各射靶 次,每次射靶的成绩如下:甲: , , , , , , , , ,
乙: , , , , , , , , ,
丙: , , , , , , , , ,
(1)、根据以上数据完成下表:平均数
中位数
方差
甲
乙
丙
(2)、根据表中数据分析,哪位运动员的成绩最稳定.并简要说明理由.21. 如图,已知: , , ,点 , 分别在 , 上,连接 ,且 , 是 上一点, 的延长线交 的延长线于点 .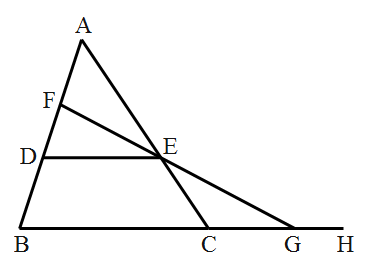 (1)、求证: ;(2)、求证: .22. 如图,在 中, , , 的重直平分线交 , 于点 , .
(1)、求证: ;(2)、求证: .22. 如图,在 中, , , 的重直平分线交 , 于点 , . (1)、求证: ;(2)、当 时,求 的面积.23. 已知:如图,在平面直角坐标系中,长方形 的顶点 的坐标是 .
(1)、求证: ;(2)、当 时,求 的面积.23. 已知:如图,在平面直角坐标系中,长方形 的顶点 的坐标是 . (1)、直接写出 点坐标( , ), 点坐标( , );(2)、如图,D为 中点.连接 , ,如果在第二象限内有一点 ,且四边形 的面积是 面积的 倍,求满足条件的点 的坐标;
(1)、直接写出 点坐标( , ), 点坐标( , );(2)、如图,D为 中点.连接 , ,如果在第二象限内有一点 ,且四边形 的面积是 面积的 倍,求满足条件的点 的坐标;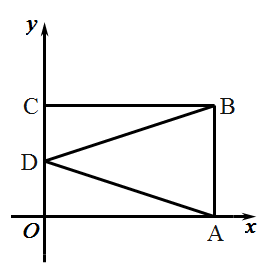 (3)、如图,动点 从点 出发,以每钞 个单位的速度沿线段 运动,同时动点 从点 出发.以每秒 个单位的連度沿线段 运动,当 到达 点时, , 同时停止运动,运动时间是 秒 ,在 , 运动过程中.当 时,直接写出时间 的值.
(3)、如图,动点 从点 出发,以每钞 个单位的速度沿线段 运动,同时动点 从点 出发.以每秒 个单位的連度沿线段 运动,当 到达 点时, , 同时停止运动,运动时间是 秒 ,在 , 运动过程中.当 时,直接写出时间 的值.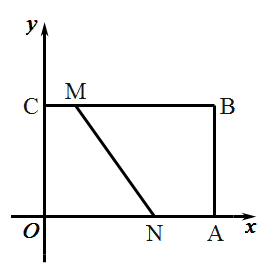 24. 如图,在平面立角坐标系 中,直线 与 轴, 轴分别交于点 、点 ,点 在 轴的负半轴上,若将 沿直线 折叠,点 恰好落在 轴正半轴上的点 处.
24. 如图,在平面立角坐标系 中,直线 与 轴, 轴分别交于点 、点 ,点 在 轴的负半轴上,若将 沿直线 折叠,点 恰好落在 轴正半轴上的点 处.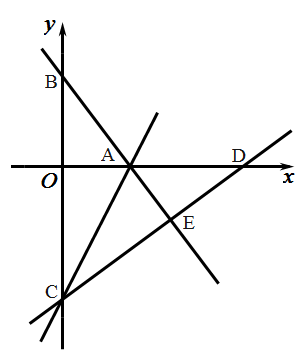 (1)、直接写出 的长;(2)、求直线 的函数表达式;(3)、求点 和点 的坐标;(4)、 轴上是否存在一点 ,使得 ?若存在,直接写出点 的坐标;若不存在,请说明理由.25. 如图,已知 , , ,斜边 , 为 垂直平分线,且 ,连接 , .
(1)、直接写出 的长;(2)、求直线 的函数表达式;(3)、求点 和点 的坐标;(4)、 轴上是否存在一点 ,使得 ?若存在,直接写出点 的坐标;若不存在,请说明理由.25. 如图,已知 , , ,斜边 , 为 垂直平分线,且 ,连接 , .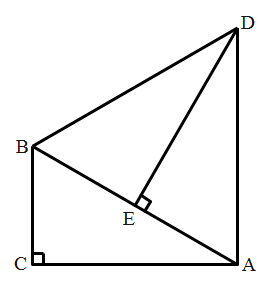 (1)、直接写出 , ;(2)、求证: 是等边三角形;(3)、如图,连接 ,作 ,垂足为点 ,直接写出 的长;
(1)、直接写出 , ;(2)、求证: 是等边三角形;(3)、如图,连接 ,作 ,垂足为点 ,直接写出 的长;
 (4)、 是直线 上的一点,且 ,连接 ,直接写出 的长.
(4)、 是直线 上的一点,且 ,连接 ,直接写出 的长.