湖北省十堰市丹江口市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-26 类型:期末考试
一、单选题
-
1. 下列图形是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在直角坐标系中,点 与点 关于 轴对称,则点 的坐标为( )A、 B、 C、 D、3. 使分式 有意义的 的取值范是( )A、 B、 C、 D、4. 下列运算正确的是:( )A、 B、 C、 D、5. 下列各式从左到右的变形中,属于因式分解的是( )A、m(a+b)=ma+mb B、a2+4a﹣21=a(a+4)﹣21 C、x2﹣1=(x+1)(x﹣1) D、x2+16﹣y2=(x+y)(x﹣y)+166. 下列式子为最简二次根式的是( )A、 B、 C、 D、7. 如图,从边长为a的正方形中去掉一个边长为b的小正方形,然后将剩余部分剪后拼成一个长方形,上述操作能验证的等式是( )
2. 在直角坐标系中,点 与点 关于 轴对称,则点 的坐标为( )A、 B、 C、 D、3. 使分式 有意义的 的取值范是( )A、 B、 C、 D、4. 下列运算正确的是:( )A、 B、 C、 D、5. 下列各式从左到右的变形中,属于因式分解的是( )A、m(a+b)=ma+mb B、a2+4a﹣21=a(a+4)﹣21 C、x2﹣1=(x+1)(x﹣1) D、x2+16﹣y2=(x+y)(x﹣y)+166. 下列式子为最简二次根式的是( )A、 B、 C、 D、7. 如图,从边长为a的正方形中去掉一个边长为b的小正方形,然后将剩余部分剪后拼成一个长方形,上述操作能验证的等式是( )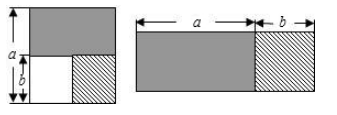 A、 B、 C、 D、8. 已知: .求作:一个角,使它等于 .步骤如下:如图,
A、 B、 C、 D、8. 已知: .求作:一个角,使它等于 .步骤如下:如图,( 1 )作射线
( 2 )以 为圆心,任意长为半径作弧,交 于 ,交 于 ;
( 3 )以 为圆心, 为半径作弧 ,交 于 ;
( 4 )以 为圆心, 为半径作弧,交弧 于 ;
( 5 )过点 作射线 .则 就是所求作的角.请回答:该作图的依据是( )

 A、 B、 C、 D、9. 下列各式从左到右的变形,一定正确的是( )A、 B、 C、 D、10. 如图,将矩形(长方形) 沿 折叠,使点 与点 重合,点 落在 处,连接 , ,则下列结论:① ,② ,③ ,④ , , 三点在同一直线上,其中正确的是( )
A、 B、 C、 D、9. 下列各式从左到右的变形,一定正确的是( )A、 B、 C、 D、10. 如图,将矩形(长方形) 沿 折叠,使点 与点 重合,点 落在 处,连接 , ,则下列结论:① ,② ,③ ,④ , , 三点在同一直线上,其中正确的是( ) A、①②③ B、①③④ C、②③④ D、①②④
A、①②③ B、①③④ C、②③④ D、①②④二、填空题
-
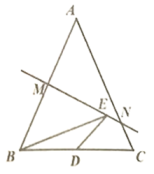
11. 现在美国麻省理工大学攻读博士学位的 后中国“天才少年”曹源经过潜心研究,发现将两层石墨烯,旋转到特定的“魔法角度”( )叠加时,它们可以在零阻力的情况下传导电子,成为超导体,他因此荣登世界顶级科学期刊《自然》,2018年度十大科学家之首!石墨烯目前是世界上最薄却也是最坚硬的纳米材料,其理论厚度仅 米,将这个数用科学记数法表示为米.12. 中 的取值范围为.13. 若 是一个完全平方式,则m的值是.14. 如图,等腰三角形 的底边 长为 ,面积是 ,腰 的垂直平分线 分别交 , 于点 、 ,若点 为底边 的中点,点 为线段 上一动点,则 的周长的最小值为.
三、解答题
-
15. 计算:(1)、 ;(2)、16. 化简:(1)、 ;(2)、17. 分解因式:(1)、(2)、(3)、18. 如图,已知 , , .

①作 关于 轴的对称图形 ;
② 为 轴上一点,请在图中找出使 的周长最小时的点 并直接写出此时点 的坐标(保留作图痕迹)
19. 如图,有一个池塘,要测池塘两端 , 的距离,可先在平地上取一个点 ,从点 不经过池塘可以直接达到点 和 ,连接 并延长到点 ,使 ,连接 并延长到点 ,使 ,连接 ,那么量出 的长度就是 , 的距离,为什么?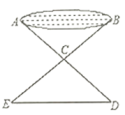 20. 先化简,再求值: ,其中 .21. 先阅读下列的解答过程,然后作答:
20. 先化简,再求值: ,其中 .21. 先阅读下列的解答过程,然后作答:形如 的化简,只要我们找到两个数 、 使 , ,
这样 , ,于是 .
例如:化简 .
解:这里 , ,由于 , ,即 , ,
.
由上述例题的方法化简:
(1)、(2)、22. 张康和李健两名运动爱好者周末相约到丹江环库绿道进行跑步锻炼.(1)、周日早上 点,张康和李健同时从家出发,分别骑自行车和步行到离家距离分别为 千米和 千米的绿道环库路入口汇合,结果同时到达,且张康每分钟比李健每分钟多行 米,求张康和李健的速度分别是多少米 分?(2)、两人到达绿道后约定先跑 千米再休息,李健的跑步速度是张康跑步速度的 倍,两人在同起点,同时出发,结果李健先到目的地 分钟.①当 , 时,求李健跑了多少分钟?
②求张康的跑步速度多少米 分?(直接用含 , 的式子表示)
23. 如图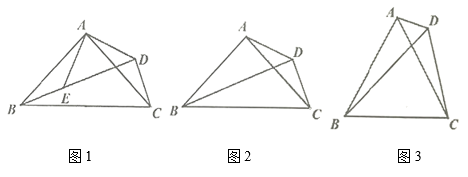 (1)、如图1,等腰 和等腰 中, , , , 三点在同一直线上,求证: ;(2)、如图2,等腰 中, , , 是三角形外一点,且 ,求证: ;(3)、如图3,等边 中, 是形外一点,且 ,
(1)、如图1,等腰 和等腰 中, , , , 三点在同一直线上,求证: ;(2)、如图2,等腰 中, , , 是三角形外一点,且 ,求证: ;(3)、如图3,等边 中, 是形外一点,且 ,① 的度数为;
② , , 之间的关系是.
24. 如图1,在平面直角坐标系中,直线 分别交 轴、 轴于点 ,点 ,且 、 满足 . (1)、求 , 的值;(2)、以 为边作 ,点 在直线 的右侧且 ,求点 的坐标;(3)、若(2)的点 在第四象限(如图2), 与 交于点 , 与 轴交于点 ,连接 ,过点 作 交 轴于点 .
(1)、求 , 的值;(2)、以 为边作 ,点 在直线 的右侧且 ,求点 的坐标;(3)、若(2)的点 在第四象限(如图2), 与 交于点 , 与 轴交于点 ,连接 ,过点 作 交 轴于点 .①求证 ;
②直接写出点 到 的距离.