河南省信阳市息县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-26 类型:期末考试
一、单选题
-
1. 下列图形中,轴对称图形的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4 -
2. 下列运算正确的是( )A、 B、 C、 D、
-
3. 一个等腰三角形两边长分别为20和10,则周长为( )A、40 B、50 C、40或50 D、不能确定
-
4. 若x2+2(m+1)x+25是一个完全平方式,那么m的值( )A、4 或-6 B、4 C、6 或4 D、-6
-
5. 如图,下列条件中,不能证明 的是( )
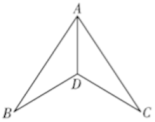 A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 , -
6. 下列各多项式相乘:①(-2ab+5x)(5x+2ab);②(ax-y)(-ax-y);③(-ab-c)(ab-c);④(m+n)(-m-n).其中可以用平方差公式的有 ( )A、4个 B、3个 C、2个 D、1个
-
7. 某细胞的直径是0.00000095米,将0.00000095用科学记数法表示为( )。A、 B、 C、 D、
-
8. 甲打字员计划用若干小时完成文稿的电脑输入工作,两小时后,乙打字员协助此项工作,且乙打字员文稿电脑输入的速度是甲的1.5倍,结果提前6小时完成任务,则甲打字员原计划完成此项工作的时间是( )A、17小时 B、14小时 C、12小时 D、10小时
-
9. 如图,以 的顶点 为圆心,适当长为半径画弧,分别交 于点 ,交 于点 ;再分别以 , 为圆心,大于 的长为半径画弧,两弧在 内部交于点 ,过点 作射线 ,连接 ,则下列说法不一定成立的是( )
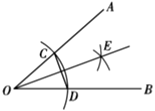 A、射线 是 的平分线 B、 是等腰三角形 C、 , 两点关于 所在直线对称 D、 , 两点关于 所在直线对称
A、射线 是 的平分线 B、 是等腰三角形 C、 , 两点关于 所在直线对称 D、 , 两点关于 所在直线对称 -
10. 如图,在等腰 ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
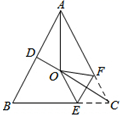 A、60° B、55° C、50° D、45°
A、60° B、55° C、50° D、45°
二、填空题
-
11. 分解因式 -2a2+8ab-8b2=.
-
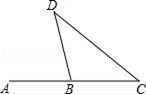
12. 如图,∠ABD=76°,∠C=38°,BC=30cm,则BD的长为 .
-
13. 已知点P(a+1,2a-3)关于x轴的对称点在第一象限,则a的取值范围是.
-
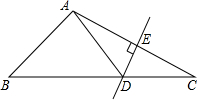
14. 如图,在△ABC中,DE是AC的垂直平分线,△ABD的周长为13,△ABC的周长为19,则AE=.
-
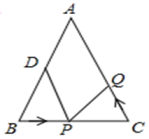
15. 如图,在Δ 中,已知 点 为 中点,点 在线段 上以每秒 的速度由 点向 点运动,同时点 在线段 上由 点向 点运动。当点 的运动速度为每秒 时,能够在某一时刻使得Δ 与Δ 全等
三、解答题
-
16. 计算下列各题:(1)、 ;(2)、 .
-
17. 解分式方程:(1)、 ;(2)、 .
-
18. 先化简,再求值 然后从-2≤x≤2的范围内选取一个合适的整数作为x的值代入求值.
-
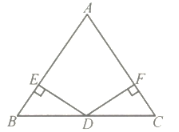
19. 如图,在△ABC中,AB=AC,BD=CD,DE AB,DF AC,垂足分别为E,F.求证:DE=DF
-
20. 如图,在平面直角坐标系中,每个小正方形的边长均为1,点 的坐标为 ,点 的坐标为 ,点 的坐标为 .
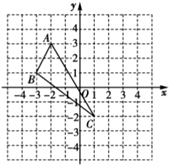
①作出 关于 轴对称的 (其中 , , 分别是 , , 的对应点,不写画法).
②直接写出 , , 三点的坐标.
③在 轴上求作一点 ,使 的值最小.(简要写出作图步骤)
-
21. 列方程或方程组解应用题:
为响应市政府“绿色出行”的号召,小张上班由自驾车改为骑公共自行车.已知小张家距上班地点10千米.他用骑公共自行车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程少45千米,他从家出发到上班地点,骑公共自行车方式所用的时间是自驾车方式所用的时间的4倍.小张用骑公共自行车方式上班平均每小时行驶多少千米?
-
22. 如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,BE=3cm,AD=9cm.
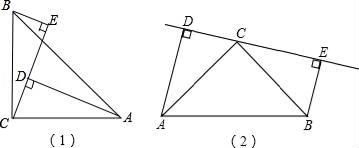
求:
(1)、DE的长;(2)、若CE在△ABC的外部(如图),其它条件不变,DE的长是多少? -
23. 如图,在平面直角坐标系中,直线 分别交 轴、 轴于点 和点 ,且 , 满足 .
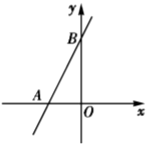 (1)、 , .(2)、点 在直线 的右侧,且 :
(1)、 , .(2)、点 在直线 的右侧,且 :①若点 在 轴上,则点 的坐标为;
②若 为直角三角形,求点 的坐标.
