广西百色市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期：2020-02-26 类型：期末考试
一、单选题
-
1. 下列图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 在平面直角坐标系中，点 在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列各图中，能表示y是x的函数的是（ ）A、
B、
C、
D、
4. 点P（1，﹣2）关于y轴对称的点的坐标是（ ）A、（1，2） B、（﹣1，2） C、（﹣1，﹣2） D、（﹣2，1）5. 如图，△ABC的一角被墨水污了，但小明很快就画出跟原来一样的图形，他所用定理是（ ）
A、SAS B、SSS C、ASA D、HL6. 已知直线y=-2x+3和直线y=kx - 5平行，则k的值为（ ）A、2 B、-2 C、3 D、无法确定7. 已知直线y=mx-4经过P（-2,-8），则m的值为（ ）A、1 B、-1 C、-2 D、28. 点P（－5，4）到y轴的距离是（ ）A、5 B、4 C、－5 D、39. 下列命题中，是假命题的是（ ）A、同旁内角互补 B、对顶角相等 C、两点确定一条直线 D、全等三角形的面积相等10. 三角形两边的长分别是4和10，则此三角形第三边的长可能是（ ）A、16 B、11 C、6 D、511. 如图，折叠直角三角形纸片的直角，使点C落在AB上的点E处，已知BC=24，∠B=30°，则DE的长是（ ）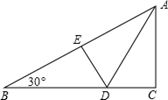
A、12 B、10 C、8 D、612. 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点(1，1)，第2次接着运动到点(2，0)，第3次接着运动到点(3，2)……按这样的运动规律，经过第2019次运动后，动点P的坐标是（ ）
A、（2018，2） B、（2019，0） C、（2019，1） D、（2019，2）二、填空题
-
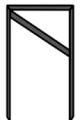
13. 函数 中，自变量x的取值范围是 ．14. 如图，木匠在做门框时防止门框变形，用一根木条斜着钉好，这样门框就固定了，所运用的数学道理是.
15. 在平面直角坐标系中，将点P（2，0）向下平移1个单位得到 ，则 的坐标为 ．16. 在△ABC中，AB=AD=CD，且∠C=40°，则∠BAD的度数为.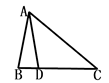
17. 如图，直线 ： 与直线 ： 相交于点P（1，2），则关于 的不等式x+1＞mx+n的解集为 ．
18. 如图，A（3，4），B（0，1），C为x轴上一动点，当△ABC的周长最小时，则点C的坐标为 ．
三、解答题
-
19. 如图，已知A（0，4），B（﹣2，2），C（3，0）．
(1)、作△ABC关于x轴对称的△A1B1C1；(2)、写出点A1 ， B1的坐标：A1 ， B1；(3)、若每个小方格的边长为1，求△A1B1C1的面积．20. 如图，两条公路相交于点O，在交角侧有A、B两个村庄，现在要建一加油站P，使得加油站P到两条公路的距离和到A、B两个村庄的距离相等，请画出加油站P的位置.（用尺规作图，保留作图痕迹，不写作法和证明过程）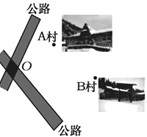
21. 如图，点D，E在△ABC的边BC上，AB=AC，BD=CE．求证：AD=AE．
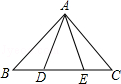22. 已知某一次函数的图象如图所示.
(1)、求这个一次函数的解析式．(2)、请直接写出该直线关于y轴对称的直线解析式．23. 如图，△ABC中，AD平分∠BAC，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC于F．
(1)、说明BE=CF的理由；(2)、如果AB=5，AC=3，求AE、BE的长．24. 在△ABC中，∠ABC和∠ACB的平分线相交于点O，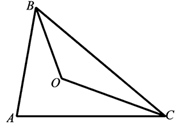
(1)、若∠ABC=60°，∠ACB=40°，求∠BOC的度数；(2)、若∠ABC=60°，OB=4，且△ABC的周长为16，求△ABC的面积25. 某电话公司开设了两种手机通讯业务，甲种业务：使用者先缴50元月租费，然后每通话1分钟，再付话费0.4元；乙种业务：不交月租费，每通话1分钟，付话费0.6元（指市话）．若一个月内通话x分钟，两种方式的费用分别为y1（元）和y2（元）．(1)、分别求出y1、y2与x之间的函数关系式．(2)、根据每月可能的通话时间，作为消费者选用哪种缴费方式更实惠．26. 如图，直线y=-x+1和直线y=x-2相交于点P，分别与y轴交于A、B两点．
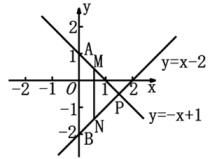(1)、求点P的坐标；(2)、求△ABP的面积；(3)、M、N分别是直线y=-x+1和y=x-2上的两个动点，且MN∥y轴，若MN=5，直接写出M、N两点的坐标．