广西壮族自治区梧州市岑溪市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-26 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列四个图案中,不是轴对称图案的是( )A、
 B、
B、 C、
C、 D、
D、 3. 以下列长度的线段为边,可以作一个三角形的是( )A、 B、 C、 D、4. 点 到 轴的距离是( )A、 B、 C、 D、5. 如图,线段 与 相交于点 ,连接 ,且 ,要使 ,应添加一个条件,不能证明 的是( )
3. 以下列长度的线段为边,可以作一个三角形的是( )A、 B、 C、 D、4. 点 到 轴的距离是( )A、 B、 C、 D、5. 如图,线段 与 相交于点 ,连接 ,且 ,要使 ,应添加一个条件,不能证明 的是( ) A、 B、 C、 D、6. 在下列命题中,真命题是( )A、相等的角是对顶角 B、同位角相等 C、三角形的外角和是 D、角平分线上的点到角的两边相等7. 如图,是岑溪市几个地方的大致位置的示意图,如果用 表示孔庙的位置,用 表示东山公园的位置,那么体育场的位置可表示为( )
A、 B、 C、 D、6. 在下列命题中,真命题是( )A、相等的角是对顶角 B、同位角相等 C、三角形的外角和是 D、角平分线上的点到角的两边相等7. 如图,是岑溪市几个地方的大致位置的示意图,如果用 表示孔庙的位置,用 表示东山公园的位置,那么体育场的位置可表示为( ) A、 B、 C、 D、8. 如图工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A、 B、 C、 D、8. 如图工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( ) A、两点之间线段最短 B、两点确定一条直线 C、三角形具有稳定性 D、长方形的四个角都是直角9. 一次函数y=﹣3x﹣2的图象和性质,表述正确的是( )A、y随x的增大而增大 B、在y轴上的截距为2 C、与x轴交于点(﹣2,0) D、函数图象不经过第一象限10. 如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )
A、两点之间线段最短 B、两点确定一条直线 C、三角形具有稳定性 D、长方形的四个角都是直角9. 一次函数y=﹣3x﹣2的图象和性质,表述正确的是( )A、y随x的增大而增大 B、在y轴上的截距为2 C、与x轴交于点(﹣2,0) D、函数图象不经过第一象限10. 如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )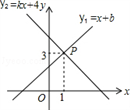 A、x>﹣2 B、x>0 C、x>1 D、x<111. 如图,在 中, 平分 于 .如果 ,那么 等于( )
A、x>﹣2 B、x>0 C、x>1 D、x<111. 如图,在 中, 平分 于 .如果 ,那么 等于( )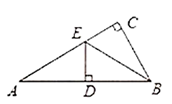 A、 B、 C、 D、12. 如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G,下列结论中正确的是( )
A、 B、 C、 D、12. 如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G,下列结论中正确的是( )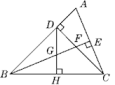
①△BCD为等腰三角形;②BF=AC;③CE= BF;④BH=CE,
A、①② B、①③ C、①②③ D、①②③④二、填空题
-
13. 在函数y= 中,自变量x的取值范围是 .14. 已知函数y=2x+m-1是正比例函数,则m=.15. 点P(2,-3)关于x轴对称的点P′的坐标是 .16. 如图, , ,则 的度数是.
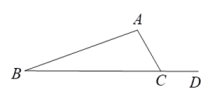 17. 如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出个.
17. 如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出个.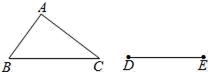 18. 如图,某园林公司承担了绿化某社区块空地的绿化任务,工人工作一段时间后,提高了工作效率.该公司完成的绿化面积 S (单位: m2 与工作时间 (单位: h )之间的函数关系如图所示,则该公司提高工作效率前每小时完成的绿化面积是 m2 .
18. 如图,某园林公司承担了绿化某社区块空地的绿化任务,工人工作一段时间后,提高了工作效率.该公司完成的绿化面积 S (单位: m2 与工作时间 (单位: h )之间的函数关系如图所示,则该公司提高工作效率前每小时完成的绿化面积是 m2 .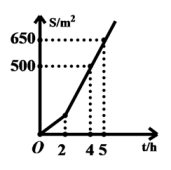
三、解答题
-
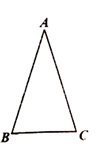
19. 如图,在 中, ,求 的度数.
 20. 如图,点B、E、C、F在一条直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
20. 如图,点B、E、C、F在一条直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.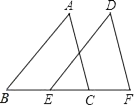 21. 如图,两个班的学生分别在C、D两处参加植树劳动,现要在道路AO、OB的交叉区域内(∠AOB的内部)设一个茶水供应点M,M到两条道路的距离相等,且MC=MD,这个茶水供应点的位置应建在何处?请说明理由。(保留作图痕迹,不写作法)
21. 如图,两个班的学生分别在C、D两处参加植树劳动,现要在道路AO、OB的交叉区域内(∠AOB的内部)设一个茶水供应点M,M到两条道路的距离相等,且MC=MD,这个茶水供应点的位置应建在何处?请说明理由。(保留作图痕迹,不写作法)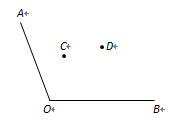 22. 在平面直角坐标系中的位置如图所示.
22. 在平面直角坐标系中的位置如图所示.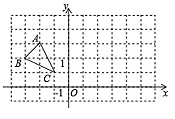
①在图中画出 关于 轴对称的图形 ,并写出顶点 的坐标;
②将 向下平移 个单位长度,再向左平移 个单位长度得到 ,画出平移后的 ,并写出顶点 的坐标.
23. 如图,在△ABC中,点D在BC边上,BD=AD=AC,E为CD的中点.若∠B=35°,求∠CAE度数.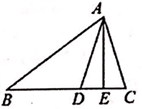 24. 如图,一次函数图象经过点 ,与 轴交于点 ,且与正比例函数 的图象交于点 , 点的横坐标是 .
24. 如图,一次函数图象经过点 ,与 轴交于点 ,且与正比例函数 的图象交于点 , 点的横坐标是 .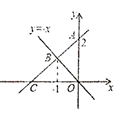 (1)、请直接写出点 的坐标( ,);(2)、求该一次函数的解析式;(3)、求 的面积.25. 如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)、请直接写出点 的坐标( ,);(2)、求该一次函数的解析式;(3)、求 的面积.25. 如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.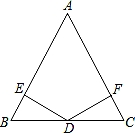 (1)、求证:△BED≌△CFD;(2)、若∠A=60°,BE=2,求△ABC的周长.26. 某公司计划购买若干台电脑,现从两家商场了解到同一种型号的电脑报价均为 元,并且多买都有一定的优惠. 各商场的优惠条件如下:
(1)、求证:△BED≌△CFD;(2)、若∠A=60°,BE=2,求△ABC的周长.26. 某公司计划购买若干台电脑,现从两家商场了解到同一种型号的电脑报价均为 元,并且多买都有一定的优惠. 各商场的优惠条件如下:甲商场优惠条件:第一台按原价收费,其余的每台优惠 ;
乙商场优惠条件:每台优惠 .
(1)、设公司购买 台电脑,选择甲商场时, 所需费用为 元,选择乙商场时,所需费用为 元,请分别求出 与 之间的关系式.(2)、什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?(3)、现在因为急需,计划从甲乙两商场一共买入 台某品牌的电脑,其中从甲商场购买 台电脑.已知甲商场的运费为每台 元,乙商场的运费为每台 元,设总运费为 元,在甲商场的电脑库存只有 台的情况下,怎样购买,总运费最少?最少运费是多少?