广西壮族自治区柳州市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-26 类型:期末考试
一、单选题
-
1. 下列银行图标中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图, 平分 , , ,垂足分别为 、 ,若 ,则 ( )
2. 如图, 平分 , , ,垂足分别为 、 ,若 ,则 ( )
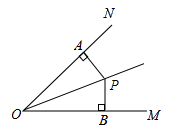 A、 B、 C、 D、3. 如图, 是 的中线,则 的面积 与 的面积 的关系是( )
A、 B、 C、 D、3. 如图, 是 的中线,则 的面积 与 的面积 的关系是( )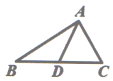 A、 B、 C、 D、无法确定4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( )
A、 B、 C、 D、无法确定4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( ) A、40° B、30° C、35° D、25°6. 科学家发现一种病毒的直径为 微米,则用科学记数法表示 为( )A、 B、 C、 D、7. 如果把分式 的 和 都扩大为原来的 倍,那么分式的值( )A、扩大为原来的 倍 B、缩小为原来的 C、不变 D、扩大为原来的 倍8. 若 是一个完全平方式,则 的取值是( )A、4 B、-4 C、 D、9. 如图,正 的边长为 ,过点 的直线 ,且 与 关于直线 对称, 为线段 上一动点,则 的最小值是( )
A、40° B、30° C、35° D、25°6. 科学家发现一种病毒的直径为 微米,则用科学记数法表示 为( )A、 B、 C、 D、7. 如果把分式 的 和 都扩大为原来的 倍,那么分式的值( )A、扩大为原来的 倍 B、缩小为原来的 C、不变 D、扩大为原来的 倍8. 若 是一个完全平方式,则 的取值是( )A、4 B、-4 C、 D、9. 如图,正 的边长为 ,过点 的直线 ,且 与 关于直线 对称, 为线段 上一动点,则 的最小值是( ) A、 B、 C、 D、10. 如图,在 中, , ,点 为 的中点,点 、 分别在 、 上,且 ,下列结论:① 是等腰直角三角形;② ;③ ;④ .其中正确的是( )
A、 B、 C、 D、10. 如图,在 中, , ,点 为 的中点,点 、 分别在 、 上,且 ,下列结论:① 是等腰直角三角形;② ;③ ;④ .其中正确的是( ) A、①②④ B、②③④ C、①②③ D、①②③④
A、①②④ B、②③④ C、①②③ D、①②③④二、填空题
-
11. 若 有意义,则x的取值范围是 .
12. 计算: .13. 一个n边形的内角和是720°,则n= .14. 如图,已知 ,要使 ,可添加一个条件 . (写出一个即可)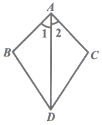 15. 若三角形的三边长分别为 , , ,则 的取值范围是 .16. 如图,点 、 分别在 的 、 边上,沿 将 翻折,点 的对应点为点 , , ,且 ,则 等于(用含 、 的式子表示).
15. 若三角形的三边长分别为 , , ,则 的取值范围是 .16. 如图,点 、 分别在 的 、 边上,沿 将 翻折,点 的对应点为点 , , ,且 ,则 等于(用含 、 的式子表示).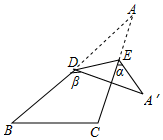
三、解答题
-
17. 计算:18. 因式分解:19. 解分式方程:20. 如图,在平面直角坐标系中,点 , , .
 (1)、作 关于 轴的对称图形 (不写作法).(2)、写出 、 、 的坐标.21. 如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
(1)、作 关于 轴的对称图形 (不写作法).(2)、写出 、 、 的坐标.21. 如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.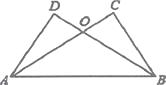
求证:
(1)、BC=AD;
(2)、△OAB是等腰三角形.
22. 某种型号油电混合动力汽车,从A地到B地燃油行驶需纯燃油费用76元,从A地到B地用电行驶需纯用电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.(1)、求每行驶1千米纯用电的费用;(2)、若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少需用电行驶多少千米?23. 如图, 是边长为6的等边三角形, 是 边上一动点,由 向 运动(与 、 不重合), 是 延长线上一动点,与点 同时以相同的速度由 向 延长线方向运动( 不与 重合),过 作 于 ,连接 交 于 .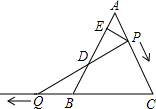 (1)、当 时,求 的长;(2)、在运动过程中线段 的长是否发生变化?如果不变,求出线段 的长;如果发生改变,请说明理由.
(1)、当 时,求 的长;(2)、在运动过程中线段 的长是否发生变化?如果不变,求出线段 的长;如果发生改变,请说明理由.