辽宁省鞍山市2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-02-26 类型:期末考试
一、单选题
-
1. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、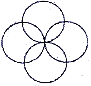 D、
D、 2. 抛物线 向左平移1个单位,再向下平移1个单位后的抛物线解析式是( )A、 B、 C、 D、3. 如图, 是 的直径,点 、 在 上,若 ,则 等于多少度( )
2. 抛物线 向左平移1个单位,再向下平移1个单位后的抛物线解析式是( )A、 B、 C、 D、3. 如图, 是 的直径,点 、 在 上,若 ,则 等于多少度( ) A、42 B、48 C、46 D、504. 如图,在 中, 是 的中点, , ,则 的长为( )
A、42 B、48 C、46 D、504. 如图,在 中, 是 的中点, , ,则 的长为( ) A、 B、4 C、 D、5. 若方程x2+3x+c=0有实数根,则c的取值范围是( )A、c≤ B、c≤ C、c≥ D、c≥6. 反比例函数 ,下列说法不正确的是( )A、图象经过点(1,-3) B、图象位于第二、四象限 C、图象关于直线y=x对称 D、y随x的增大而增大7. 已知二次函数y=x2﹣2x+m(m为常数)的图象与x轴的一个点为(3,0),则关于x的一元二次方程x2﹣2x+m=0的两个实数根是( )A、x1=﹣1,x2=3 B、x1=1,x2=3 C、x1=﹣1,x2=1 D、x1=3,x2=﹣58. 如图,在Rt△ABC中,∠C=90°,点P是边AC上一点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,BD平分∠ABC,以下四个结论①△BQD是等腰三角形;②BQ=DP;③PA= QP;④ =(1+ )2;其中正确的结论的个数( )
A、 B、4 C、 D、5. 若方程x2+3x+c=0有实数根,则c的取值范围是( )A、c≤ B、c≤ C、c≥ D、c≥6. 反比例函数 ,下列说法不正确的是( )A、图象经过点(1,-3) B、图象位于第二、四象限 C、图象关于直线y=x对称 D、y随x的增大而增大7. 已知二次函数y=x2﹣2x+m(m为常数)的图象与x轴的一个点为(3,0),则关于x的一元二次方程x2﹣2x+m=0的两个实数根是( )A、x1=﹣1,x2=3 B、x1=1,x2=3 C、x1=﹣1,x2=1 D、x1=3,x2=﹣58. 如图,在Rt△ABC中,∠C=90°,点P是边AC上一点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,BD平分∠ABC,以下四个结论①△BQD是等腰三角形;②BQ=DP;③PA= QP;④ =(1+ )2;其中正确的结论的个数( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 抛物线y=(x﹣3)2﹣2的顶点坐标是 .10. 如图,一组平行横格线,其相邻横格线间的距离都相等,已知点A、B、C、D、O都在横格线上,且线段AD,BC交于点O,则AB:CD等于 .
 11. 庆“元旦”,市工会组织篮球比赛,赛制为单循环形式(每两队之间都赛一场),共进行了45场比赛,求这次有多少队参加比赛?若设这次有x队参加比赛,则根据题意可列方程为 .12. 如图,将一个顶角为30°角的等腰△ABC绕点A顺时针旋转一个角度α(0<α<180°)得到△AB'C′,使得点B′、A、C在同一条直线上,则α等于°.
11. 庆“元旦”,市工会组织篮球比赛,赛制为单循环形式(每两队之间都赛一场),共进行了45场比赛,求这次有多少队参加比赛?若设这次有x队参加比赛,则根据题意可列方程为 .12. 如图,将一个顶角为30°角的等腰△ABC绕点A顺时针旋转一个角度α(0<α<180°)得到△AB'C′,使得点B′、A、C在同一条直线上,则α等于°.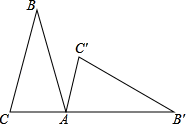 13. 如图,在⊙O中,AB是⊙O的弦,CD是⊙O的直径,CD⊥AB于点M,若AB=CM=4,则⊙O的半径为 .
13. 如图,在⊙O中,AB是⊙O的弦,CD是⊙O的直径,CD⊥AB于点M,若AB=CM=4,则⊙O的半径为 . 14. 如图,在平面直角坐标系中,已知点E(﹣4,2),F(﹣1,﹣1).以原点O为位似中心,把△EFO扩大到原来的2倍,则点E的对应点E'的坐标为 .
14. 如图,在平面直角坐标系中,已知点E(﹣4,2),F(﹣1,﹣1).以原点O为位似中心,把△EFO扩大到原来的2倍,则点E的对应点E'的坐标为 . 15. 如图,在平面直角坐标系中,菱形OABC的边OA在x轴的负半轴上,反比例函数y= (x<0)的图象经过对角线OB的中点D和顶点C.若菱形OABC的面积为6,则k的值等于 .
15. 如图,在平面直角坐标系中,菱形OABC的边OA在x轴的负半轴上,反比例函数y= (x<0)的图象经过对角线OB的中点D和顶点C.若菱形OABC的面积为6,则k的值等于 .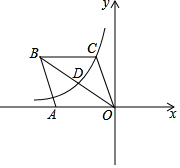 16. 如图,抛物线解析式为y=x2 , 点A1的坐标为(1,1),连接OA1;过A1作A1B1⊥OA1 , 分别交y轴、抛物线于点P1、B1;过B1作B1A2⊥A1B1分别交y轴、抛物线于点P2、A2;过A2作A2B2⊥B1A2 , 分别交y轴、抛物线于点P3、B2…;则点Pn的坐标是 .
16. 如图,抛物线解析式为y=x2 , 点A1的坐标为(1,1),连接OA1;过A1作A1B1⊥OA1 , 分别交y轴、抛物线于点P1、B1;过B1作B1A2⊥A1B1分别交y轴、抛物线于点P2、A2;过A2作A2B2⊥B1A2 , 分别交y轴、抛物线于点P3、B2…;则点Pn的坐标是 .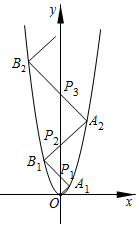
三、解答题
-
17. 用适当的方法解下列一元二次方程(1)、x2+2x=3;(2)、2x2﹣6x+3=0.18. 如图,已知△ABC的顶点A、B、C的坐标分别是A(﹣1,﹣1)、B(﹣4,﹣3)、C(﹣4,﹣1).

①画出△ABC关于原点O中心对称的图形△A1B1C1;
②将△ABC绕点A按顺时针方向旋转90°后得到△AB2C2 , 画出△AB2C2并求线段AB扫过的面积.
19. 某公司2016年10月份营业额为64万元,12月份营业额达到100万元,(1)、求该公司11、12两个月营业额的月平均增长率;(2)、如果月平均增长率保持不变,据此估计明年1月份月营业额.20. 已知关于x的一元二次方程x2+(2k+1)x+k2=0有实数根.(1)、求k的取值范围.(2)、设方程的两个实数根分别为x1、x2 , 若2x1x2﹣x1﹣x2=1,求k的值.21. 如图,在△ABC中,D为AC上一点,E为CB延长线上一点,且 ,DG∥AB,求证:DF=BG. 22. 如图,直线l的解析式为y= x,反比例函数y= (x>0)的图象与l交于点N,且点N的横坐标为6.
22. 如图,直线l的解析式为y= x,反比例函数y= (x>0)的图象与l交于点N,且点N的横坐标为6. (1)、求k的值;(2)、点A、点B分别是直线l、x轴上的两点,且OA=OB=10,线段AB与反比例函数图象交于点M,连接OM,求△BOM的面积.23. 如图,在△ABC中,点O为BC边上一点,⊙O经过A、B两点,与BC边交于点E,点F为BE下方半圆弧上一点,FE⊥AC,垂足为D,∠BEF=2∠F.
(1)、求k的值;(2)、点A、点B分别是直线l、x轴上的两点,且OA=OB=10,线段AB与反比例函数图象交于点M,连接OM,求△BOM的面积.23. 如图,在△ABC中,点O为BC边上一点,⊙O经过A、B两点,与BC边交于点E,点F为BE下方半圆弧上一点,FE⊥AC,垂足为D,∠BEF=2∠F. (1)、求证:AC为⊙O切线.(2)、若AB=5,DF=4,求⊙O半径长.24. 2019年鞍山市出现了猪肉价格大幅上涨的情况,经过对我市某猪肉经销商的调查发现,当猪肉售价为60元/千克时,每天可以销售80千克,日销售利润为1600元(不考虑其他因素对利润的影响):售价每上涨1元,则每天少售出2千克;若设猪肉售价为x元/千克,日销售量为y千克.(1)、求y关于x的函数解析式(不要求写出自变量的取值范围);(2)、若物价管理部门规定猪肉价格不高于68元/千克,当售价是多少元/千克时,日销售利润最大,最大利润是多少元.25. 如图,BD是平行四边形ABCD的对角线,DE⊥AB于点E,过点E的直线交BC于点G,且BG=CG.
(1)、求证:AC为⊙O切线.(2)、若AB=5,DF=4,求⊙O半径长.24. 2019年鞍山市出现了猪肉价格大幅上涨的情况,经过对我市某猪肉经销商的调查发现,当猪肉售价为60元/千克时,每天可以销售80千克,日销售利润为1600元(不考虑其他因素对利润的影响):售价每上涨1元,则每天少售出2千克;若设猪肉售价为x元/千克,日销售量为y千克.(1)、求y关于x的函数解析式(不要求写出自变量的取值范围);(2)、若物价管理部门规定猪肉价格不高于68元/千克,当售价是多少元/千克时,日销售利润最大,最大利润是多少元.25. 如图,BD是平行四边形ABCD的对角线,DE⊥AB于点E,过点E的直线交BC于点G,且BG=CG. (1)、求证:GD=EG.(2)、若BD⊥EG垂足为O,BO=2,DO=4,画出图形并求出四边形ABCD的面积.(3)、在(2)的条件下,以O为旋转中心顺时针旋转△GDO,得到△G′D'O,点G′落在BC上时,请直接写出G′E的长.26. 如图,直线y=﹣ x+1与x轴,y轴分别交于A,B两点,抛物线y=ax2+bx+c过点B,并且顶点D的坐标为(﹣2,﹣1).
(1)、求证:GD=EG.(2)、若BD⊥EG垂足为O,BO=2,DO=4,画出图形并求出四边形ABCD的面积.(3)、在(2)的条件下,以O为旋转中心顺时针旋转△GDO,得到△G′D'O,点G′落在BC上时,请直接写出G′E的长.26. 如图,直线y=﹣ x+1与x轴,y轴分别交于A,B两点,抛物线y=ax2+bx+c过点B,并且顶点D的坐标为(﹣2,﹣1). (1)、求该抛物线的解析式;(2)、若抛物线与直线AB的另一个交点为F,点C是线段BF的中点,过点C作BF的垂线交抛物线于点P,Q,求线段PQ的长度;(3)、在(2)的条件下,点M是直线AB上一点,点N是线段PQ的中点,若PQ=2MN,直接写出点M的坐标.
(1)、求该抛物线的解析式;(2)、若抛物线与直线AB的另一个交点为F,点C是线段BF的中点,过点C作BF的垂线交抛物线于点P,Q,求线段PQ的长度;(3)、在(2)的条件下,点M是直线AB上一点,点N是线段PQ的中点,若PQ=2MN,直接写出点M的坐标.