江苏省盐城市建湖县2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-02-26 类型:期末考试
一、单选题
-
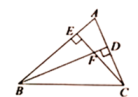
1. 已知⊙O的半径为10cm,OP=8cm,则点P和⊙O的位置关系是( )A、点P在圆内 B、点P在圆上 C、点P在圆外 D、无法判断2. 一组数据1,2,8,5,3,9,5,4,5,4的众数、中位数分别为( )A、4.5、5 B、5、4.5 C、5、4 D、5、53. 给出下列各组线段,其中成比例线段的是( )A、 B、 C、 D、4. 在 中, , , ,则 的值为( )A、 B、 C、 D、5. 关于抛物线 ,下列说法中错误的是( )A、开口方向向下 B、对称轴是直线 C、当 时, 随 的增大而增大 D、顶点坐标为6. 如图,在 中,高 相交于点 ,图中与 相似的三角形共有( )
 A、1个 B、2个 C、3个 D、4个7. 如图,平面直角坐标系中,点 ,以原点 为位似中心,把 缩小为 ,且 与 的相似比为 ,则点 的对应点 的坐标为( )
A、1个 B、2个 C、3个 D、4个7. 如图,平面直角坐标系中,点 ,以原点 为位似中心,把 缩小为 ,且 与 的相似比为 ,则点 的对应点 的坐标为( ) A、 B、 或 C、 D、 或8. 如图,二次函数 的图象与 轴交于 两点,点 位于 、 之间,与 轴交于点 ,对称轴为直线 ,直线 与抛物线 交于 两点, 点在 轴上方且横坐标小于5,则下列结论:① ;② ;③ (其中 为任意实数);④ ,其中正确的是( )
A、 B、 或 C、 D、 或8. 如图,二次函数 的图象与 轴交于 两点,点 位于 、 之间,与 轴交于点 ,对称轴为直线 ,直线 与抛物线 交于 两点, 点在 轴上方且横坐标小于5,则下列结论:① ;② ;③ (其中 为任意实数);④ ,其中正确的是( )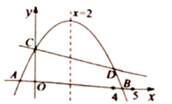 A、①②③④ B、①②③ C、①②④ D、①③④
A、①②③④ B、①②③ C、①②④ D、①③④二、填空题
-
9. 已知线段AB的长为10米,P是AB的黄金分割点(AP>BP),则AP的长米.(精确到0.01米)10. 若 ,则 的值为.11. 一组数据0,1,2,3,4的方差是.12. 一个不透明的口袋中共有8个白球、5个黄球、5个绿球、2个红球,这些球除颜色外都相同。从口袋中随机摸出一个球,这个球是白球的概率是.13. 如图抛物线y=ax2+bx+c的对称轴是x=﹣1,与x轴的一个交点为(﹣5,0),则不等式ax2+bx+c>0的解集为 .
 14. 如图, 分别是 的边 延长线上的点,且 , .已知 , ,则 .
14. 如图, 分别是 的边 延长线上的点,且 , .已知 , ,则 . 15. 如图,在 的正方形方格图形中,小正方形的顶点称为格点, 的顶点都在格点上,则 的余弦值是 .
15. 如图,在 的正方形方格图形中,小正方形的顶点称为格点, 的顶点都在格点上,则 的余弦值是 .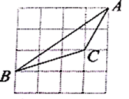 16. 如图,有一个横截面边缘为抛物线的水泥门洞,门洞内的地面宽度为 ,两侧离地面 高处各有一盏灯,两灯间的水平距离为 ,则这个门洞的高度为 .(精确到 )
16. 如图,有一个横截面边缘为抛物线的水泥门洞,门洞内的地面宽度为 ,两侧离地面 高处各有一盏灯,两灯间的水平距离为 ,则这个门洞的高度为 .(精确到 )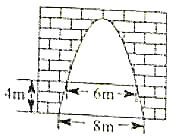
三、解答题
-
17. 计算:18. 已知关于 的方程 .(1)、求证:不论 取何实数,此方程都有两个不相等的实数根;(2)、若此方程的一个根为 ,求 的值.19. 某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲
10
6
10
6
8
乙
7
9
7
8
9
经过计算,甲进球的平均数为8,方差为3.2.
(1)、求乙进球的平均数和方差;(2)、如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?20. 将图中的 型(正方形)、 型(菱形)、 型(等腰直角三角形)纸片分别放在 个盒子中,盒子的形状、大小、质地都相同,再将这 个盒子装入一只不透明的袋子中. (1)、搅匀后从中摸出 个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是;(2)、搅匀后先从中摸出 个盒子(不放回),再从余下的 个盒子中摸出 个盒子,把摸出的 个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)21. 学校打算用长20米的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠在长为12米的墙上,面积为42平方米,求生物园的长和宽.
(1)、搅匀后从中摸出 个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是;(2)、搅匀后先从中摸出 个盒子(不放回),再从余下的 个盒子中摸出 个盒子,把摸出的 个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)21. 学校打算用长20米的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠在长为12米的墙上,面积为42平方米,求生物园的长和宽. 22. 如图,小超想要测量窗外的路灯 的高度.星期天晚上,他发现灯光透过窗户照射在房间的地板上,窗户的最高点 落在地板 处、窗户的最低点落在地板是 处,小超测得窗户距地面的高度 ,窗高 ,并测得 , .请根据以上测量数据,求窗外的路灯 的高度.
22. 如图,小超想要测量窗外的路灯 的高度.星期天晚上,他发现灯光透过窗户照射在房间的地板上,窗户的最高点 落在地板 处、窗户的最低点落在地板是 处,小超测得窗户距地面的高度 ,窗高 ,并测得 , .请根据以上测量数据,求窗外的路灯 的高度.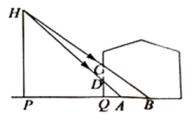 23. 如图,在等腰 中, , , 是 上一点,若 .
23. 如图,在等腰 中, , , 是 上一点,若 .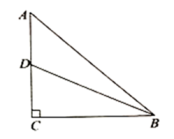 (1)、求 的长;(2)、求 的值.24. 如图,在 中, ,以 为直径的 分别与 交于点 ,过点 作 于点 .
(1)、求 的长;(2)、求 的值.24. 如图,在 中, ,以 为直径的 分别与 交于点 ,过点 作 于点 . (1)、求证: 是 的切线;(2)、求证: ;(3)、若 , ,求 的长.25. 如图,在四边形 中, , , , 为 边上一点(不与 重合),连接 ,过 点作 交 于 ,使得 .
(1)、求证: 是 的切线;(2)、求证: ;(3)、若 , ,求 的长.25. 如图,在四边形 中, , , , 为 边上一点(不与 重合),连接 ,过 点作 交 于 ,使得 .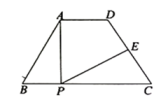 (1)、 与 相似吗?为什么?(2)、若 ,求 的长;(3)、当 为多少时, 的长最大?最大为多少?26. 某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)、 与 相似吗?为什么?(2)、若 ,求 的长;(3)、当 为多少时, 的长最大?最大为多少?26. 某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.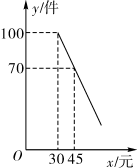 (1)、求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;(2)、若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?(3)、若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?27. 如图,抛物线 过 , 两点.
(1)、求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;(2)、若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?(3)、若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?27. 如图,抛物线 过 , 两点.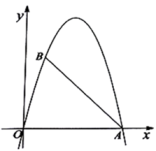

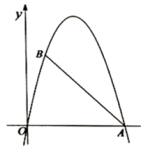
备用图1 备用图2
(1)、求该抛物线的解析式;(2)、点 是抛物线上一点,且位于第一象限,当 的面积为6时,求点 的坐标;(3)、在线段 右侧的抛物线上是否存在一点 ,使得 分 的面积为 两部分?存在,求出点 的坐标;不存在,请说明理由.