江苏省盐城市东台市第二联盟2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-02-26 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程2x²+5x＝6的二次项系数、一次项系数、常数项分别是（）

A、2，5，6 B、5，2，﹣6 C、2，-5，6 D、2，5，﹣6

查看试题解析
2. 已知△ABC中，∠C=90°，若AC= $\sqrt{3}$ ，BC=1，则sinA的值是（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
3. 压岁钱由来已久，古称“厌胜钱”、“压祟钱”等．铛铛同学在2019年春节共收到10位长辈给的压岁钱，分别是：100元、200元、100元、50元、400元、300元、50元、100元、200元、400元．关于这组数据，下列说法正确的是（）

A、中位数是200元 B、众数是100元 C、平均数是200元 D、极差是300元

查看试题解析
4. 已知抛物线y=x²﹣x﹣2经过点（m，5），则m²﹣m+2的值为（）

A、7 B、8 C、9 D、10

查看试题解析
5. 已知圆锥的高为 $\sqrt{3}$ ，高所在的直线与母线的夹角为 $30^{\circ}$ ，则圆锥的侧面积为 $($ $)$

A、 $π$ B、 $1.5 π$ C、 $2 π$ D、 $3 π$

查看试题解析
6. 如图①，点C在线段AB上以每秒1个单位长度的速度由A向B运动，运动到点B时停止，过点C作AB的垂线l，在AB上方的垂线l上取一点D，且满足∠ADB＝90°．设点C运动的时间为x，△ABD的面积为y，图②是y随x变化的函数关系的大致图象，则线段AB的长为（）

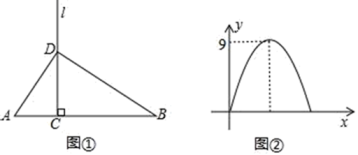A、9 B、6 C、3 $\sqrt{2}$ D、2 $\sqrt{2}$

查看试题解析

二、填空题

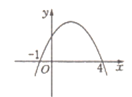
7. 一元二次方程（x﹣1）（x+2）=0的根是．

查看试题解析
8. 一个扇形的半径长为5，且圆心角为60°，则此扇形的弧长为．

查看试题解析
9. 已知线段a＝4 cm，b＝9 cm，则线段a，b的比例中项为cm．

查看试题解析
10. 如图是二次函数y=ax²+bx+c的图像，已知点(2，y₁)，(3，y₂)是函数图象上的两个点，则y₁ ， y₂的大小关系是。

查看试题解析
11. 在一个不透明的空袋子里放入3个白球和2个红球，每个球除颜色外完全相同，小乐从中任意摸出1个球，摸出的球是红球，放回后充分摇匀，又从中任意摸出1个球，摸到红球的概率是．

查看试题解析
12. 如图，身高是1.6m的某同学直立于旗杆影子的顶端处，测得同一时刻该同学和旗杆的影子长分别为1.2m和9m.则旗杆的高度为m.

查看试题解析
13. 如图，点G是 $△ ABC$ 的重心，AG的延长线交BC于点D，过点G作 $GE / / BC$ 交AC于点E，如果 $BC = 6$ ，那么线段GE的长为．

查看试题解析
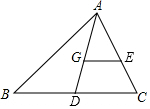14. 如图，⊙O是△ABC的外接圆，已知∠ABO=40°，则∠ACB的大小为．

查看试题解析
15. 若a≠b，且 $a^{2} - 4 a + 1 = 0, b^{2} - 4 b + 1 = 0$ 则 $\frac{1}{1 + a^{2}} + \frac{1}{1 + b^{2}}$ 的值为

查看试题解析
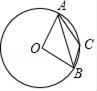16. 如图，在等腰Rt△ABC中，∠BAC＝90°，AB＝AC，BC＝4 $\sqrt{2}$ ，点D是AC边上一动点，连接BD，以AD为直径的圆交BD于点E，则线段CE长度的最小值为.

查看试题解析
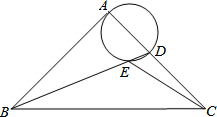17. 某市努力改善空气质量，近年来空气质量明显好转，根据该市环境保护局公布的2010﹣2014这五年各年全年空气质量优良的天数如表所示，根据表中信息回答：

2010

2011

2012

2013

2014

234

233

245

247

256

(1)、这五年的全年空气质量优良天数的中位数是，平均数是；

(2)、这五年的全年空气质量优良天数与它前一年相比增加最多的是年（填写年份）；

(3)、求这五年的全年空气质量优良天数的方差．

查看试题解析

三、解答题

18. 计算： $\sqrt{4} + {(- \frac{1}{2})}^{- 1} - 2 cos 60 ° + {(2 - π)}^{0}$ .

查看试题解析
19. 如图，已知抛物线与x轴交于点A（﹣1，0），E（3，0）两点，与y轴交于点B（0，3）．

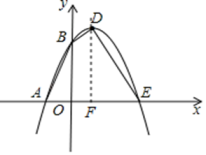(1)、求抛物线的解析式；

(2)、设抛物线的顶点为D，求四边形AEDB的面积．

查看试题解析
20. 已知如图，△ABC中，AB＝AC，用尺规在BC边上求作一点P，使△BPA∽△BAC（保留作图痕迹，不写作法）.

查看试题解析
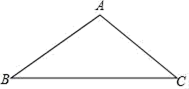21. 在一个不透明的袋子里有1个红球，1个黄球和n个白球，它们除颜色外其余都相同．

(1)、从这个袋子里摸出一个球，记录其颜色，然后放回，摇均匀后，重复该实验，经过大量实验后，发现摸到白球的频率稳定于0.5左右，求n的值；

(2)、在（1）的条件下，先从这个袋中摸出一个球，记录其颜色，放回，摇均匀后，再从袋中摸出一个球，记录其颜色．请用画树状图或者列表的方法，求出先后两次摸出不同颜色的两个球的概率．

查看试题解析
22. 已知关于x的一元二次方程x²+2（m﹣1）x+m²﹣3＝0有两个不相等的实数根．

(1)、求m的取值范围；

(2)、若m为非负整数，且该方程的根都是无理数，求m的值．

查看试题解析
23. 为积极参与文明城市创建活动，我市某校在教学楼顶部新建了一块大型宣传牌，如下图。小明同学为测量宣传牌的高度AB，他站在距离教学楼底部E处6米远的地面C处，测得宣传牌的底部B的仰角为60°，同时测得教学楼窗户D处的仰角为30°（A、B、D、E在同一直线上）。然后，小明沿坡度i=1：1.5的斜坡从C走到F处，此时DF正好与地面CE平行。

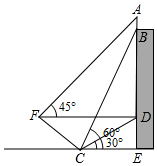(1)、求点F到直线CE的距离（结果保留根号）；

(2)、若小明在F处又测得宣传牌顶部A的仰角为45°，求宣传牌的高度AB（结果精确到0.1米， $\sqrt{2} \approx 1.41 ， \sqrt{3} \approx 1.73$ ）。

查看试题解析
24. 如图，在△ABC中，∠A＝45°，以AB为直径的⊙O经过AC的中点D，E为⊙O上的一点，连接DE，BE，DE与AB交于点F.

(1)、求证：BC为⊙O的切线；

(2)、若F为OA的中点，⊙O的半径为2，求BE的长.

查看试题解析
25. 如图，在Rt△ABC中，∠C＝90°，AC＝12cm，BC＝24cm．动点P从点A开始沿边AC向点C以2cm/s的速度移动；动点Q从点C开始沿边CB向点B以4cm/s的速度移动．如果P，Q两点同时出发．

(1)、经过几秒，△PCQ的面积为32cm²？

(2)、若设△PCQ的面积为S，运动时间为t，请写出当t为何值时，S最大，并求出最大值；

(3)、当t为何值时，以P，C，Q为顶点的三角形与△ABC相似？

查看试题解析
26. 定义：在一个三角形中，若存在两条边x和y，使得y＝x² ，则称此三角形为“平方三角形”，x称为平方边．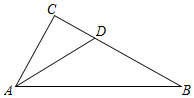

(1)、“若等边三角形为平方三角形，则面积为 $\frac{\sqrt{3}}{4}$ 是命题；“有一个角为30°且有一条直角边为2的直角三角形是平方三角形”是命题；（填“真”或“假”）

(2)、若a，b，c是平方三角形的三条边，平方边a＝2，若三角形中存在一个角为60°，求c的值；

(3)、如图，在△ABC中，D是BC上一点．
①若∠CAD＝∠B，CD＝1，求证，△ABC是平方三角形；

②若∠C＝90°，BD＝1，AC＝m，CD＝n，求tan∠DAB．（用含m，n的代数式表示）

查看试题解析
27. 如图，已知：抛物线y＝a（x+1）（x﹣3）与x轴相交于A、B两点，与y轴的交于点C（0，﹣3）．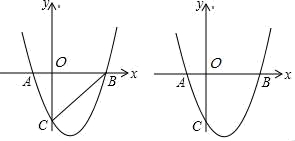

(1)、求抛物线的解析式的一般式．

(2)、若抛物线上有一点P，满足∠ACO＝∠PCB，求P点坐标．

(3)、直线l：y＝kx﹣k+2与抛物线交于E、F两点，当点B到直线l的距离最大时，求△BEF的面积．

查看试题解析

2010	2011	2012	2013	2014
234	233	245	247	256