江苏省常州市2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-02-26 类型:期末考试
一、单选题
-
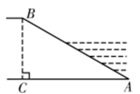
1. 已知x=2是关于x的一元二次方程x2+ax=0的一个根,则a的值为( )A、-2 B、2 C、 D、2. 某同学对数据26,36,36,46,5■,52进行统计分析.发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、平均数 B、中位数 C、方差 D、众数3. 河堤横断面如图所示,斜坡AB的坡度=1: ,AB= 6m,则BC的长是( )
 A、 m B、3m C、 m D、6m4. 若两个相似三角形的周长比为1:3,则它们的面积比为( )A、1:9 B、1:6 C、1:3 D、6:15. 如果圆锥的底面半径为3,母线长为6,那么它的侧面积等于( )A、9π B、18π C、24π D、36π6. 如图⊙P经过点A(0, )、O(0,0)、B(1,0),点C在第一象限的 上,则∠BCO的度数为( )
A、 m B、3m C、 m D、6m4. 若两个相似三角形的周长比为1:3,则它们的面积比为( )A、1:9 B、1:6 C、1:3 D、6:15. 如果圆锥的底面半径为3,母线长为6,那么它的侧面积等于( )A、9π B、18π C、24π D、36π6. 如图⊙P经过点A(0, )、O(0,0)、B(1,0),点C在第一象限的 上,则∠BCO的度数为( )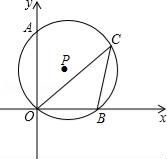 A、15° B、30° C、45° D、60°7. 如图,△ABC和阴影三角形的顶点都在小正方形的顶点上,则与△ABC相似的阴影三角形为( )
A、15° B、30° C、45° D、60°7. 如图,△ABC和阴影三角形的顶点都在小正方形的顶点上,则与△ABC相似的阴影三角形为( )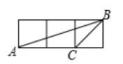 A、
A、 B、
B、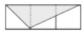 C、
C、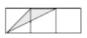 D、
D、 8. 某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为10的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是( )
8. 某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为10的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
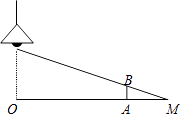
9. 若2a=3b,则a:b=.10. 若 是锐角,且 ,则 .11. 不透明袋子中有2个红球和4个蓝球,这些球除颜色外无其他差别,从袋子中随机取出1个球是红球的概率是.12. 如图,电线杆上的路灯距离地面8m,身高1.6m的小明(AB)站在距离电线杆的底部(点O)20m的A处,则小明的影子AM长为m.
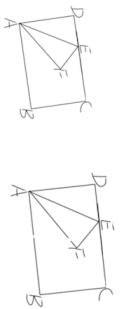
 13. 某楼盘2018年初房价为每平方米20000元,经过两年连续降价后,2020 年初房价为16200元。设该楼盘这两年房价年平均降低的百分率为x,根据题意可列方程为.14. 关于x的一元二次方程(2-k) x2-2x+1=0有两个不相等的实数根,则整数k的最小值是.15. 如图,AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上,斜边过点B,一条直角边交该半圆于点Q.若AB=2,则线段BQ的长为.
13. 某楼盘2018年初房价为每平方米20000元,经过两年连续降价后,2020 年初房价为16200元。设该楼盘这两年房价年平均降低的百分率为x,根据题意可列方程为.14. 关于x的一元二次方程(2-k) x2-2x+1=0有两个不相等的实数根,则整数k的最小值是.15. 如图,AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上,斜边过点B,一条直角边交该半圆于点Q.若AB=2,则线段BQ的长为.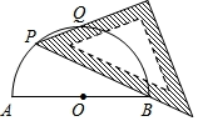 16. 如图,在平面直角坐标系中,以O为圆心,6为半径画圆弧,与两坐标轴分别交于点A、B,已知点C(5, 0)、D(0, 3),P为AB上一点,则2PD+CP的最小值为.
16. 如图,在平面直角坐标系中,以O为圆心,6为半径画圆弧,与两坐标轴分别交于点A、B,已知点C(5, 0)、D(0, 3),P为AB上一点,则2PD+CP的最小值为.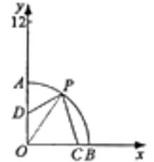
三、解答题
-
17.
(1)、解方程: x(x-4)=5;
(2)、求值: tan245°- 2cos60°.18. 如图,在平面直角坐标系x O y中,△ABC 三个顶点坐标分别为A (1, 2),B(7,2),C(5,6). (1)、在图中画出△ABC外接圆的圆心P;(2)、圆心P的坐标是;(3)、tan∠ACB=.19. 某中学在“书香校园”活动中,为了解学生的读书情况,学校抽样调查了部分同学在一周内的阅读时间,绘制如下统计图.根据图中信息,解答下列问题:
(1)、在图中画出△ABC外接圆的圆心P;(2)、圆心P的坐标是;(3)、tan∠ACB=.19. 某中学在“书香校园”活动中,为了解学生的读书情况,学校抽样调查了部分同学在一周内的阅读时间,绘制如下统计图.根据图中信息,解答下列问题: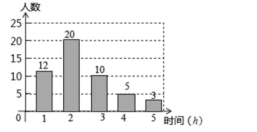 (1)、被抽查学生阅读时间的中位数为h,平均数为h;(2)、若该校共有2000名学生,请你估算该校一周内阅读时间不少于3h的学生人数.20. 小明放学回家看到桌上有一盘小麻糕,妈妈说当中有芝麻馅、肉馅各1个,青菜馅2个,这些小麻糕除馅外无其他差别.(1)、小明随机从盘中取出一个小麻糕,取出的是芝麻馅的概率是.(2)、小明随机从盘中一次取出两个小麻糕,试用画树状图或列表的方法表示所有可能的结果,并求取出的两个都是青菜馅的概率.21. 如图,在矩形ABCD中,AB:BC=1:2, 点E在AD上,且ED=3AE.判断△ABC与△EAB是否相似,并说明理由.
(1)、被抽查学生阅读时间的中位数为h,平均数为h;(2)、若该校共有2000名学生,请你估算该校一周内阅读时间不少于3h的学生人数.20. 小明放学回家看到桌上有一盘小麻糕,妈妈说当中有芝麻馅、肉馅各1个,青菜馅2个,这些小麻糕除馅外无其他差别.(1)、小明随机从盘中取出一个小麻糕,取出的是芝麻馅的概率是.(2)、小明随机从盘中一次取出两个小麻糕,试用画树状图或列表的方法表示所有可能的结果,并求取出的两个都是青菜馅的概率.21. 如图,在矩形ABCD中,AB:BC=1:2, 点E在AD上,且ED=3AE.判断△ABC与△EAB是否相似,并说明理由.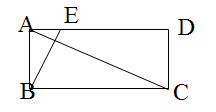 22. 如图,用长6m的铝合金条制成“日”字形窗框,窗框的宽和高各是多少时,窗户的透光面积为1.5m2 (铝合金条的宽度不计) ?
22. 如图,用长6m的铝合金条制成“日”字形窗框,窗框的宽和高各是多少时,窗户的透光面积为1.5m2 (铝合金条的宽度不计) ? 23. 如图,AB是⊙O的切线,切点为B,OA交⊙O于点C,且AC=OC.
23. 如图,AB是⊙O的切线,切点为B,OA交⊙O于点C,且AC=OC.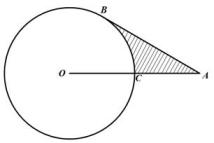 (1)、求弧BC的度数;(2)、设⊙O的半径为5,求图中阴影部分的面积.
(1)、求弧BC的度数;(2)、设⊙O的半径为5,求图中阴影部分的面积.